Next: Office hours
Richard Melrose
Department of Mathematics, Massachusetts Institute of Technology
Tuesday and Thursdays, 1-2:30 in Room 4-102. The book is Adams and Guillemin [1]
Read A-G, Chapter 1, pages 1-4, 24-26.
Problems, A-G, Chapter 1, p.11, Problems 1, 2; p;39 Problems 1 (first part), 2 Here are the problems
1.1.1. Prove that the set
![]() of Bernoulli sequences is
uncountable by the Cantor diagonal argument.
of Bernoulli sequences is
uncountable by the Cantor diagonal argument.
1.1.2. a) Let
![]() Show that
Show that ![]() can be written in the form
can be written in the form
![]() with
with ![]() or
or ![]() Show
that this expansion is unique when we restrict to nonterminating series.
Show
that this expansion is unique when we restrict to nonterminating series.
b) Show that for any (positive) integer ![]()
![]() can be
written in the form
can be
written in the form
![]() where
where
![]() Show that the expansion is unique when we restrict
to nonterminating series.
Show that the expansion is unique when we restrict
to nonterminating series.
1.3.1. Let ![]() be an uncountable set. Let
be an uncountable set. Let
![]() be the collection
of all finite subsets of
be the collection
of all finite subsets of ![]() Given
Given
![]() let
let ![]() be the number of elements in
be the number of elements in ![]() Show that
Show that
![]() is a ring
and that
is a ring
and that ![]() is a measure on
is a measure on
![]()
1.3.2. Let ![]() be an infinite set and let
be an infinite set and let
![]() be the collection
of sets consisting of the finte sets and the complements, in
be the collection
of sets consisting of the finte sets and the complements, in ![]() of
finte sets. Let
of
finte sets. Let ![]() be the function
be the function ![]() if
if ![]() is finite,
is finite,
![]() if the complement of
if the complement of ![]() is finite. Is
is finite. Is ![]() a measure?
a measure?
Read A-G, pp 27-31, pp 4-9
Problems: p.39, nos. 3, 4; p.12 nos. 4,5. Here are the problems
1.3.3. a) Let ![]() be an infinte set and
be an infinte set and
![]() the collection of all
countable subsets of
the collection of all
countable subsets of ![]() Is
Is
![]() a ring?
a ring?
b) Let ![]() be a measure on
be a measure on
![]() Show that there exists a
function
Show that there exists a
function
![]() such that
such that
c) Show that the funcion ![]() in part b) has the following two
properties. (1) the set
in part b) has the following two
properties. (1) the set
![]() is countable and (2)
is countable and (2)
![]()
d) Show that if ![]() has the properties in part c) the formula
(1) defies a measure on
has the properties in part c) the formula
(1) defies a measure on
![]()
1.3.4. Let ![]() be the real line and
be the real line and
![]() Given
Given
![]() let
let ![]() if, for some positive
if, for some positive
![]()
![]() contains the interval
contains the interval
![]() and otherwise
and otherwise
![]() Show that
Show that ![]() is an additive set function but is
not countably additive.
is an additive set function but is
not countably additive.
1.1.4. Show that
1.1.5. Define the Rademacher functions on the whole real line by requiring
them to be periodice of period one - so setting
![]() With this definition show that
With this definition show that
![]() and by
induction,
and by
induction,
![]()
Countable additivity and subadditivity
Outer measure
Sets of measure zero
Measurable sets
Rademacher functions
(Special) Chebyshev's inequality
Weak law of large numbers
Homework due Friday 20th: Chapter 1, p. 41, nos 11, 13; p. 42 nos 19, 20.
A-G, pp 33-39.
The ![]() -ring of measurable sets.
-ring of measurable sets.
The law of large numbers.
A-G pp 53-58.
Measurable functions
Countable additivity: Theorem 11.
Proof of Theorem 11 finished.
Monotone convergence.
Additivity for positive functions.
The space
![]() of integrable functions (on
of integrable functions (on ![]() with
respect to the measure
with
respect to the measure ![]() on the
on the ![]() -ring
-ring
![]()
Linearity of the integrable on integrable functions.
A-G pages 77-80.
Fatou's lemma (for a sequence of non-negative measurable functions
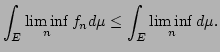
Lebesgue's Dominated convergence theorem. Pointwise convergence of a sequence of measurable functions with absolute value bounded by a fixed integrabe function implies convergence of the integrals to the integral of the limit.
The Banach space
![]()
The Banach space
![]() continued.
continued.
A Hilbert space,
![]()
Hilbert spaces
Bessel's inequality
Existence of a complete orthonormal basis in a separable Hilbert space.
Outline of proof that an ![]() function on
function on
![]() is determined
by its Fourier coefficients.
is determined
by its Fourier coefficients.
Equality of Riemann and Lebesgue integrals of a continuous function
on ![]()
Convergence of the Fourier series of a function a differentiable function.
Parallelogram law in a Hilbert space; converse explained but not done.
A non-emtpy closed convex set in Hilbert space has a unique point closest to the origin.
Linear functions on a normed space are continuous if and only if they are bounded.
Riesz Representation Theorem:- Any continuous linear functional on a
Hilbert space is of the form
![]() for
some
for
some ![]()
Schwartz functions
Fourier transform
Inverse transform
Metric on the space of Schwartz functions
Density of Scwhartz functions in
![]()
Extension of Fourier transform to
![]()
Density of Schwartz functions in
![]()
Harmonic oscillator, creation and annihilation operators.
Invariance under Fourier transform.
Completeness of eigenfunctions.
Weak solutions.