I have decided to make the first test open-book, but only copies of Adams
and Guillemin are permitted, no papers or other writings.
- Set
![$ X =[0,1]\times[0,1],$](img313.png) the unit square in
the unit square in
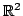 and
suppose that
and
suppose that
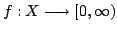 is Lebesgue measurable and
such that
is Lebesgue measurable and
such that
Show that
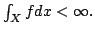
- Without using the equality of Riemann and Lebesgue integrals show
that
and
- Give, with proofs, an example of a non-negative Lesbesgue measurable
function on
![$ [0,1]$](img319.png) which has finite Lebesgue integral but is not bounded.
which has finite Lebesgue integral but is not bounded.
- Explain why the formula
defines a countably additive finite measure on the 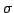 -ring,
-ring,
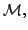 of all Lebesgue measurable subsets of
of all Lebesgue measurable subsets of
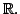 Show that completion
of
Show that completion
of
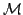 with respect to this measure is just
with respect to this measure is just
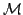 again.
again.
- Let
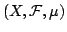 be a measure space and suppose that
be a measure space and suppose that
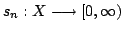 is an increasing (i.e. pointwise
non-decreasing) sequence of simple measurable functions with
is an increasing (i.e. pointwise
non-decreasing) sequence of simple measurable functions with
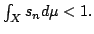 Show that the set consisting of those points
Show that the set consisting of those points 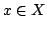 where
where
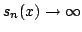 has
has 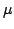 -measure zero.
-measure zero.
Richard B. Melrose
2004-05-24