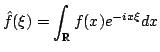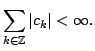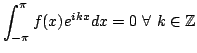This test is closed book. You are not permitted to bring any books, notes
or such material with you. You may use theorems, lemmas and propositions
from the book or from class.
There are only four questions on the actual Test.
- If
![$ f_n\in L^1([0,1])$](img402.png) is a convergent sequence with respect to the
is a convergent sequence with respect to the
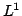 norm show that there is a subsequence which converges
pointwise almost everywhere on
norm show that there is a subsequence which converges
pointwise almost everywhere on ![$ [0,1].$](img403.png)
- (Adams and Guillemin 11, p.129) Let
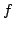 be a continuously
differentiable function on
be a continuously
differentiable function on ![$ [0,1],$](img376.png) show that
show that
- If
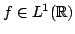 show that its Fourier transform
is continuous.
show that its Fourier transform
is continuous.
- Suppose that
![$ f\in L^2([-\pi,\pi])$](img407.png) has Fourier coefficients satisfying
Show that there is a continuous function on
has Fourier coefficients satisfying
Show that there is a continuous function on 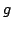 on
on
![$ [-\pi,\pi]$](img48.png) such that
such that
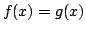 for almost all
for almost all
![$ x\in[-\pi,\pi].$](img410.png)
- Show that if
![$ f:[-\pi,\pi]\longrightarrow \mathbb{C}$](img411.png) is a bounded
measurable function which satisfies
is a bounded
measurable function which satisfies
![$ \int_{[-\pi,\pi]}x^kf(x)dx=0$](img412.png) for
all non-negative integers
for
all non-negative integers
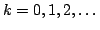 then
then 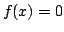 for almost all
for almost all
![$ x\in[-\pi,\pi].$](img410.png)
- Show that a continuous function
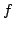 on
on
![$ [-\pi,\pi]$](img48.png) which satisfies
vanishes identically.
which satisfies
vanishes identically.
Richard B. Melrose
2004-05-24