Next: Homework Up: Lecture Notes Previous: Lecture Notes
We will use the completeness of
![]() proved last week. Let
proved last week. Let
![]() be a Cauchy sequence in
be a Cauchy sequence in
![]() Consider first the set
Consider first the set ![]() where at least one of the
where at least one of the ![]() 's is non-zero. This is a countable union of
measurable sets, hence measurable. It is in fact a countable union of sets of
finite measure, for instance
's is non-zero. This is a countable union of
measurable sets, hence measurable. It is in fact a countable union of sets of
finite measure, for instance
Now that we have our putative limit we can use Fatou's Lemma. Applied to
the sequence of measurable, non-negative, functions
![]() with
with ![]() fixed and
fixed and
![]() it states that
it states that
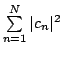 has an upper bound independent of
has an upper bound independent of
See if you can show that the limit
![]() is
independent of the order chosen for
is
independent of the order chosen for ![]()
Thus we can proceed by induction to define an orthonormal set, which will
either be finite or countable (depending on ![]() In either case it is
complete. To see this, suppose there is some element
In either case it is
complete. To see this, suppose there is some element ![]() orthogonal
to all the
orthogonal
to all the ![]() By the density of
By the density of ![]() for any
for any
![]() there
exists
there
exists ![]() such that
such that
![]() However,
However, ![]() is in the
(finite) span of the
is in the
(finite) span of the ![]() so
so
![]() This however
implies, by Pythagorus' theorem, that
This however
implies, by Pythagorus' theorem, that
![]() Thus
Thus
![]() so in fact
so in fact
![]() and hence
and hence ![]() proving the completeness.
proving the completeness.
![]()
So I need to go back and check some version of their equality. The following will do for present purposes.
This argument only needs slight modification to show that every Riemann
integrable function on ![]() is Lebesgue integrable and that the
integrals are equal; it is done in Adams and Guillemin.
is Lebesgue integrable and that the
integrals are equal; it is done in Adams and Guillemin.
Thus we know that the Fourier functions
![]() do indeed form a
countable orthonormal set for
do indeed form a
countable orthonormal set for
![]() We still need to know that
it is complete. This involves some more work.
We still need to know that
it is complete. This involves some more work.
However this will take some work.
![\begin{lemma}
If $f\in L^1([a,b])$\ for a finite interval
$[a,b]\subset \bbR$\ ...
... then the
corresponding functions $g_i\to g$\ uniformly on $[a,b].$
\end{lemma}](img218.png)
Before worrying about the proof of this, let us apply it to ![]() and
and
![]() for some
for some
![]() On the left in
(26) the inner integral is our definition of
On the left in
(26) the inner integral is our definition of ![]() in
(25) except for the missing constant. On the right in
(26) we compute, using equality of Riemann and Lebesgue
integrals for continuous functions, finding
in
(25) except for the missing constant. On the right in
(26) we compute, using equality of Riemann and Lebesgue
integrals for continuous functions, finding
![$\displaystyle \int_{[a,b]} (\int_{[x,b]}\exp(-ins)ds)f(x)dx=0,\ 0\not=n\in\bbZ$](img232.png) if if |
(26) |
We have to prove (26). Again this is a return to
basics. Notice first that both sides of (26) do make sense
if
![]() since then the integrated functions
since then the integrated functions
Now, (26) is separately linear in ![]() and
and ![]() So as
usual we can assume these functions are positive, by first replacing the
functions by their real and imaginary parts, and then their positive and negative
parts. On the left the we can take a sequence of non-negative simple functions
approaching
So as
usual we can assume these functions are positive, by first replacing the
functions by their real and imaginary parts, and then their positive and negative
parts. On the left the we can take a sequence of non-negative simple functions
approaching ![]() from below and we get convergence in
from below and we get convergence in
![]() Similarly on the right the integrated functions approach
Similarly on the right the integrated functions approach ![]() uniformly so the integrals converge. The same argument works for
uniformly so the integrals converge. The same argument works for ![]() so
it suffices to prove (26) for simple functions and hence,
again using linearity, for the characteristic functions of two measurable
sets,
so
it suffices to prove (26) for simple functions and hence,
again using linearity, for the characteristic functions of two measurable
sets,
![]()
![]() measurable. Recalling what it
means to be measurable, we can approximate say
measurable. Recalling what it
means to be measurable, we can approximate say ![]() in measure, by a
sequence of elementary sets, each a finite union of disjoint
intervals. Using Lemma 1 (several times) the resulting
integrals converge. Applying the same arguement to
in measure, by a
sequence of elementary sets, each a finite union of disjoint
intervals. Using Lemma 1 (several times) the resulting
integrals converge. Applying the same arguement to ![]() it suffices to
prove (26) when
it suffices to
prove (26) when ![]() and
and ![]() are the characteristic
functions of intervals. In this case our identity has become rather
trivial, except that we have to worry about the various cases. So, suppose
that
are the characteristic
functions of intervals. In this case our identity has become rather
trivial, except that we have to worry about the various cases. So, suppose
that ![]() is the characteristic function of
is the characteristic function of
![]() a subinterval of
a subinterval of
![]() (open, half-open or closed does not matter of course). We are
trying to prove
(open, half-open or closed does not matter of course). We are
trying to prove
![\begin{theorem}
If $h$\ is differentiable on
$[-\pi,\pi]$\ (so only from the ri...
...(h)(x)\longrightarrow h(x)\ \forall\ x\in[-\pi,\pi].
\end{equation}\end{theorem}](img270.png)
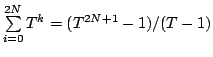 where
where
The reason for looking at ![]() is that, from (36),
is that, from (36),
I should have commented a little on the case
![]()
Richard B. Melrose 2004-05-24