Next: Grades Up: 18.103, Spring 2004 Previous: Practice Final
This exam is closed book, no books, papers or recording devices permitted. You may use theorems from class, or the book, provided you can recall them correctly.
With short solutions and comments. I hope I did not damage too many delicate egos with this final!
Suppose
![]() and
and ![]() for all
for all
![]() Show that
Show that
![]() for all
for all ![]() with
with
![]() implies that
implies that ![]() almost everywhere with
respect to Lebesgue measure.
almost everywhere with
respect to Lebesgue measure.
Generally well done.
Ans:- From a standard result, ![]() a.e. in
a.e. in ![]() for every
for every
![]() The subset of
The subset of
![]() on which
on which
![]() is therefore the union of a countable collection of sets of
measure zero, so also of measure zero. Hence
is therefore the union of a countable collection of sets of
measure zero, so also of measure zero. Hence ![]() almost everywhere in
almost everywhere in
![]()
Suppose ![]() is a bounded and self-adjoint operator on a Hilbert space
is a bounded and self-adjoint operator on a Hilbert space ![]() show that if
show that if
![]() for all
for all ![]() then
then ![]()
Only one person got this right. I did not say compact, so you cannot use the spectral theory of compact operators. No, all bounded operators are not compact etc.
Ans:- For any ![]() expanding using sesquilinearity (and linearity of
expanding using sesquilinearity (and linearity of
![]() gives
gives
Give an example of an element of
![]() which is not the Fourier
transform of an element of
which is not the Fourier
transform of an element of
![]()
Of course, I confused people by giving a harder version of this on the practice final.
Ans. If the Fourier transform of
![]() is in
is in ![]() then it
must be the inverse Fourier transform of an
then it
must be the inverse Fourier transform of an ![]() function, hence
continuous. Thus it suffices to find an
function, hence
continuous. Thus it suffices to find an ![]() function which is not
continuous, say the characteristic function of
function which is not
continuous, say the characteristic function of ![]()
If
![]() show that
show that
Generally well done although quite a few people tried to use Fourier series.
Ans:- By the translation-invariance of Lebesgue measure and countable
additivity, the terms,
![]() for
for
![]() in the
series satisfy
in the
series satisfy
![$\displaystyle \sum\limits_{j\in\mathbb{Z}}\int_{[-\pi,\pi]}\vert v_j\vert dx= \sum\limits_{\mathbb{R}}\vert u\vert dx<\infty.$](img556.png) |
Show that there is no function
![]() satisfying
satisfying
Mostly people got this one.
Ans:- If there is such a function its real part also satisfies the
condition, so we can assume it is real. Then the integral in
(![]() ) is
) is ![]() times the imaginary part of the
times the imaginary part of the ![]() th Fourier
coefficient, thus
th Fourier
coefficient, thus
![]() which series diverges, violating
Bessel's inequality.
which series diverges, violating
Bessel's inequality.
Show that the function
![]() is in
is in
![]() and
that its Fourier transform is infinitely differentiable. Is
and
that its Fourier transform is infinitely differentiable. Is ![]() a
Schwartz function?
a
Schwartz function?
Many people thought this function was Schwartz, it is not infinitely differentiable and that is one of the requirements!
Ans: Certainly
![]() and we know (if you like from class)
that
and we know (if you like from class)
that
![]() for every
for every
![]() Since follows
that
Since follows
that
![]() is continuous for every
is continuous for every ![]() No, it is
not Schwartz.
No, it is
not Schwartz.
Suppose
![]() is such that
is such that
![]() and
the Fourier transform is such that
and
the Fourier transform is such that
![]() Show that there exists a function
Show that there exists a function
![]() such that
such that
Many people got this one at least more-or-less right. However, many of the arguments to justify the integration by parts were dubious to say the least.
Ans:- Since
![]() is given, we only need to find
is given, we only need to find
![]() satisfying
satisfying
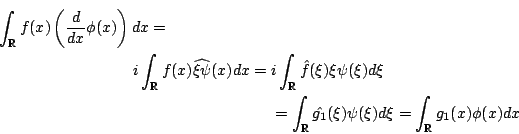
If
![]() show that
show that
One can argue directly as I did in the practice exam and show that ![]() has
equismall tail with respect to the Fourier basis when
has
equismall tail with respect to the Fourier basis when
![]() Or
Or
Ans:- If one sets
![]() when
when
![]()
![]() and zero
otherwise one gets a function in
and zero
otherwise one gets a function in
![]() sucht that
sucht that
![$\displaystyle Au(x)=\int_{[0,1]} F(x,t)u(t)dt.$](img587.png) |
Show that there exists an element
![]() which has
which has
![]() but
but
![]() for every
for every
![]()
Rather a lot of wild things said here.
Ans:- If
![]() then its Fourier transform is
Schwartz and conversely. We also know that
then its Fourier transform is
Schwartz and conversely. We also know that
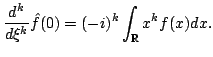 |
Richard B. Melrose 2004-05-24