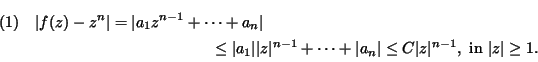For ![]() and
and ![]() an integer, define the singular
an integer, define the singular ![]() -cube
-cube
![]() by
by
Show that there is a singular
Solution: Define
![]() by
by
This looks simpler in complex notation for
Its boundary consists of four 1-cubes, up to sign. Namely:
since the last two 1-cubes are actually the same.
If ![]() is a singular
is a singular ![]() -cube in
-cube in
![]() with
with
![]() show that there is an integer
show that there is an integer ![]() such that
such that
![]() for some
for some ![]() -chain
-chain ![]() Hint:
First partition
Hint:
First partition ![]() so that each
so that each
![]() is contained on one
side of some line through
is contained on one
side of some line through ![]()
Solution: We define a continuous function
![]() so that
so that
To do so, let
for some
It follows that
| with |
Now the function
Now define a 2-cube by
![\begin{multline*}
d(t,s)=((s\vert c(t)\vert+(1-s))\cos(2\pi(s\theta(t)+(1-s)nt))...
...1-s))\sin(2\pi(s\theta(t)+(1-s)nt))), (s,t)\in[0,1]\times[0,1].
\end{multline*}](img62.png)
This
since the two terms from
[Notice this actually gives a cube ![]() with boundary
with boundary
![]() you were only asked for a chain
you were only asked for a chain ![]() so you could do it in pieces.]
so you could do it in pieces.]
(Independence of parameterization.) Let ![]() be a singular
be a singular ![]() -cube and
-cube and
![]() a
a ![]() -
-![]() function such that
function such that
![]() and
and
![]() for all
for all
![]() If
If ![]() is a
is a ![]() -form, show that
-form, show that
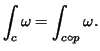 |
Solution: By definition
![$\displaystyle \int_c\omega=\int_{[0,1]^k}c^*\omega=\int{[0,1]^k}f, c^*\omega=f(x)dx^1\wedge\cdots\wedge dx^k$](img78.png) |
and similarly
![\begin{multline*}
\int_{c\circ p}\omega=\int_{[0,1]^k}(c\circ p)^*\omega=\int_{[...
...f(x)dx^1\wedge\cdots\wedge dx^k)
=gdx^1\wedge\cdots\wedge dx^k.
\end{multline*}](img79.png)
Thus
since
![$\displaystyle \int_{[0,1]^k}g=\int_{[0,1]^k}(f\circ p)\vert\det p'\vert=\int_{[0,1]^k}f.$](img83.png) |
Show that
![]() and use Stokes' theorem to conclude
that
and use Stokes' theorem to conclude
that
![]() for any
for any ![]() -chain in
-chain in
![]() Here
Here
is a smooth
Solution: If we substitute the definition of ![]()
![]()
![]() we find that
we find that
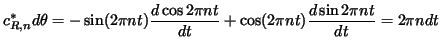 |
Thus
![$\displaystyle \int_{c_{R,n}}d\theta=\int_{[0,1]}c_{R,n}^*d\theta=\int_0^12\pi ndt=2\pi n.$](img92.png) |
It follows that
![]() for any
for any ![]() -chain
-chain ![]() in
in
![]() if
if ![]() since by Stokes' theorem this
would imply
since by Stokes' theorem this
would imply
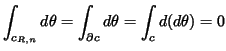 |
since
Show that the integer ![]() of Problem 4-24 is unique. This integer is called
the winding number of
of Problem 4-24 is unique. This integer is called
the winding number of ![]() around
around ![]()
Solution: If ![]() is a closed
is a closed ![]() -cube in
-cube in
![]() then with
then with ![]() from
Problem 4-24 above, using Stokes' theorem
from
Problem 4-24 above, using Stokes' theorem
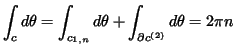 |
which shows that
Recall that the set of complex number,
![]() is simply
is simply
![]() with
with
![]() If
If
![]() let
let
![]() be
be
Define the singular
- Show that
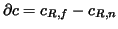 and that
and that
![$\displaystyle c([0,1]\times[0,1])\subset\mathbb{C}\setminus\{0\}$](img109.png)
if is large enough.
is large enough.
- Using Problem 4-26 above, prove the Fundamental theorem of
algebra: Every polynomal
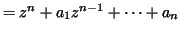 with
with
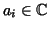 has a root in
has a root in
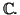
Solution
- By definition
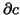 is the sum of four
is the sum of four 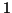 -cubes
-cubes
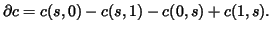
The last two are the same -cube with opposite signs, since both
-cube with opposite signs, since both
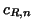 and
and 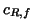 are closed.
are closed.
- We can estimate
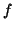 by
by
This shows that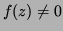 on
on 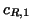 for
for 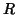 large enough. Moreover
for each
large enough. Moreover
for each ![$ s\in[0,1]$](img122.png) consider
consider
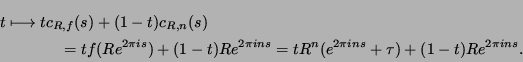
Here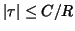 is very small by (2). Thus the straight line
given by varying
is very small by (2). Thus the straight line
given by varying ![$ t\in[0,1]$](img125.png) does not pass through the origin, so
does not pass through the origin, so
![$ c([0,1]\times[0,1])\subset\mathbb{C}\setminus\{0\}.$](img126.png)
- Since
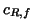 and
and 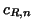 differ by an exact
differ by an exact 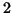 -chain in
-chain in
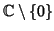 it follows from Problem 4-16 that
it follows from Problem 4-16 that
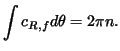
Now suppose, to get a contradiction, that
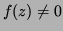 for all
for all
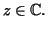 In particular,
In particular, 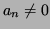 since otherwise
since otherwise 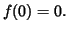 Then
Then
![$\displaystyle d(s,t)=f\circ c_{Rs,1}(t)\in\mathbb{C}\setminus\{0\} \forall (t,s)\in[0,1]\times[0,1].$](img132.png)
Since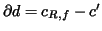 where
where 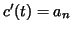 is constant it follows from
Stokes' theorem that
is constant it follows from
Stokes' theorem that
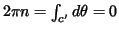 which is a
contradiction. This proves the Fundamental Theorem of Algebra, that
which is a
contradiction. This proves the Fundamental Theorem of Algebra, that 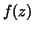 must have a zero.
must have a zero.