Next: Solutions to Problem set Up: Solutions Previous: Solutions
Chapter 2: Problem 10
This is the `discrete metric' on a set. Certainly
![]() is well defined and
is well defined and ![]() iff
iff ![]() Symmetry,
Symmetry,
![]() is immediate from the definition and the
triangle inequality
is immediate from the definition and the
triangle inequality
All subsets are open, since if
![]() and
and ![]() then
then ![]() and
and
![]() implies
implies ![]() and hence
and hence ![]() Since the complements of open
sets are closed it follows that all subsets are closed. The only compact
subsets are finite. Indeed if
Since the complements of open
sets are closed it follows that all subsets are closed. The only compact
subsets are finite. Indeed if
![]() is compact then the open balls
of radius
is compact then the open balls
of radius ![]() with centers in
with centers in ![]() cover
cover ![]() and each contains only one
point of
and each contains only one
point of ![]() so the existence of a finite subcover implies that
so the existence of a finite subcover implies that ![]() itself
is finite.
itself
is finite.
Chapter 2: Problem 12
We are to show that
![]() is compact as a subset of
is compact as a subset of
![]() directly from the definition of compactness. So, let
directly from the definition of compactness. So, let ![]()
![]() be an open cover of
be an open cover of ![]() It follows that
It follows that
![]() for some
for some
![]() But since
But since ![]() is open it contains some ball of radius
is open it contains some ball of radius
![]() around
around ![]() Thus all the points
Thus all the points
![]() for
for ![]() For each
For each
![]() we can find some
we can find some ![]() such that
such that
![]() since the
since the
![]() cover
cover ![]() Thus we have found a finite subcover
Thus we have found a finite subcover
Chapter 2: Problem 16
Here
![]() is the metric space, with
is the metric space, with
![]() the `usual'
metric. Set
the `usual'
metric. Set
To see that ![]() is not compact, recall that if it were compact as a subset
of
is not compact, recall that if it were compact as a subset
of
![]() it would be compact as a subset of
it would be compact as a subset of
![]() by Theorem 2.33. Since
it is not closed as a subset of
by Theorem 2.33. Since
it is not closed as a subset of
![]() it cannot be compact. Alternatively,
for a direct proof of non-compactness, take the open cover given by the
open sets
it cannot be compact. Alternatively,
for a direct proof of non-compactness, take the open cover given by the
open sets
![]() This can have no finite
subcover since
This can have no finite
subcover since ![]() contains points arbitrarily close to the real point
contains points arbitrarily close to the real point
![]()
Yes ![]() is open in
is open in
![]() since it is of the form
since it is of the form
![]() where
where
![]() is open, so Theorem 2.30 applies.
is open, so Theorem 2.30 applies.
Chapter 2: Problem 22
We need to show that the set of rational points,
![]() is dense in
is dense in
![]() We can use the fact that
We can use the fact that
![]() is dense. Thus, given
is dense. Thus, given
![]() and
and
![]() there exists
there exists
![]() such that
such that
![]() for each
for each
![]() Thus, as points
in
Thus, as points
in
![]()
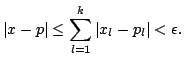 is separable since we know that
is separable since we know that
Chapter 2: Problem 23
We are to show that a given separable metric space, ![]() has a countable
base. The hint is to choose a countable dense subset
has a countable
base. The hint is to choose a countable dense subset ![]() and then to
consider the collection,
and then to
consider the collection,
![]() of all open subsets of
of all open subsets of ![]() of the
form
of the
form ![]() where
where ![]() and
and
![]() This is a countable union,
over
This is a countable union,
over
![]() of countable sets so is countable. Now, we need to show that
this is a base. So, suppose
of countable sets so is countable. Now, we need to show that
this is a base. So, suppose
![]() is a given open set. If
is a given open set. If ![]() then for some
then for some ![]()
![]() since it is open. Also, by the
density of
since it is open. Also, by the
density of ![]() in
in ![]() there exists some
there exists some ![]() with
with
![]() But
then
But
then
![]() implies
implies
![]() Thus
Thus
![]() It follows that
It follows that
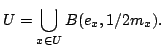 is written as a union of the elements of
is written as a union of the elements of
Chapter 2: Problem 25
We wish to show that a given compact metric space ![]() has a countable
base. As the hint says, for each
has a countable
base. As the hint says, for each
![]() consider the balls of radius
consider the balls of radius
![]() around each of the points of
around each of the points of ![]()
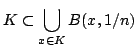 is in one of these balls at least. Now the compactness
of
is in one of these balls at least. Now the compactness
of 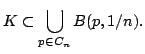 This is countable, being a countable
union of finite sets. Now it follows that
This is countable, being a countable
union of finite sets. Now it follows that 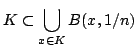 and
and
Alternatively one can see directly that the ![]()
![]() form an
open base.
form an
open base.
Richard B. Melrose 2004-05-18