Nothing due May 11. The last homework was going to be a little project in
doing a piece of mathematics but it is too late given the fact
that there will be a final exam. To test yourself and see if you have
gained in understanding from the course, try to write all this out as
clearly as you can after you figure it out.
Read Rudin Chapter 9, ``The contraction principle'' on
your own. Let
![$ F:[0,1]\times\mathbb{R}$](img54.png) be continuous and Lipschitz
continuous in the second variable, meaning that there is a constant
be continuous and Lipschitz
continuous in the second variable, meaning that there is a constant
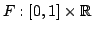 such that
such that
![$\displaystyle \vert F(x,y)-F(x,z)\vert\le C\vert y-z\vert\ \forall\ x\in[0,1],\ y,z\in\mathbb{R}.$](img56.png) |
(2) |
Suppose that for some 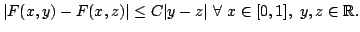
![$ f:[c,c+\delta ]\longrightarrow \mathbb{R}$](img58.png) is a differentiable function, with
is a differentiable function, with
![$ [c,c+\delta ]\subset[0,1],$](img59.png) satisfying
the differential equation
satisfying
the differential equation
![$\displaystyle f'(x)=F(x,f(x))\ \forall\ x\in [c,c+\delta ].$](img60.png) |
(3) |
- Show that
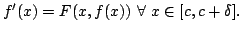 is continuously differentiable on
is continuously differentiable on
![$ [c,c+\delta]$](img62.png) and that it
satisfies the integral equation
and that it
satisfies the integral equation
![$\displaystyle f(x)=f(c)+\int_c^xF(t,f(t))dt\ \forall\ x\in[c,c+\delta ].$](img63.png) |
(4) |
- Conversely show that if
![$ f:[c,c+\delta ]\longrightarrow \mathbb{R}$](img58.png) is a
continuous function which satisfies (4) then it is
differentiable and satisfies (3).
is a
continuous function which satisfies (4) then it is
differentiable and satisfies (3).
- Fix some real number
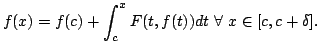 and
show that
and
show that
![$\displaystyle S=\{f\in\mathcal{C}([c,c+\delta]);f(c)=y\}\subset\mathcal{C}([c,c+\delta ])$](img65.png) |
(5) |
is closed with respect to the supremum metric.
- For
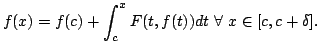 and
and 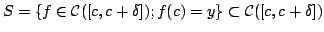 as above show that the map
as above show that the map
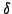 |
(6) |
defines a map from 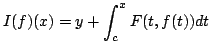 into
into 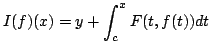 and that this map satisfies
and that this map satisfies
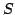 |
(7) |
where 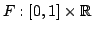 is the constant in (2).
is the constant in (2).
- Conclude that for
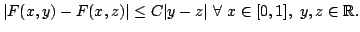 sufficiently small (depending only on
sufficiently small (depending only on 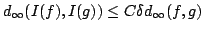 and
and
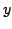 but not
but not 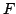 there is a unique differentiable function on
there is a unique differentiable function on
![$ [c,c+\delta]$](img62.png) satisfying
satisfying
![$\displaystyle f'(x)=F(x,f(x))\ \forall\ x\in[c,c+\delta],\ f(c)=y.$](img73.png) |
(8) |
- No big hints for the last part! Show that, given
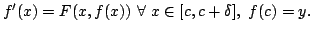 and under the same conditions as above there is a unque differentiable
function on
and under the same conditions as above there is a unque differentiable
function on ![$ [0,1]$](img75.png) satisfying the intial value problem
satisfying the intial value problem
![$\displaystyle f'(x)=F(x,f(x))\ \forall\ x\in[0,1],\ f(0)=y.$](img76.png) |
(9) |
![]() be continuous and Lipschitz
continuous in the second variable, meaning that there is a constant
be continuous and Lipschitz
continuous in the second variable, meaning that there is a constant
![]() such that
such that
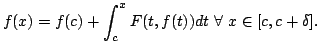 and
show that
and
show that
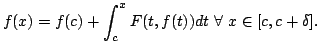 and
and 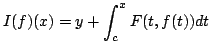 into
into 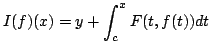 and that this map satisfies
and that this map satisfies