(Also available as postscript and acrobat file
off my web page).
The test on Thursday will be open book - just the book, nothing else is
permitted (and no notes in your book!) Note that where
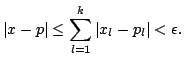 is
mentioned below the standard metric is assumed.
is
mentioned below the standard metric is assumed.
- Let
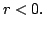 be closed. Show that there is a point
be closed. Show that there is a point 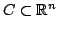 such that
such that
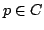
- Give a counterexample to each of the following statements:
- Subsets of
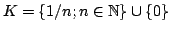 are either open or closed
are either open or closed
- A closed and bounded subset of a metric space is compact.
- In any metric space the complement of a connected set is connected.
- Given a sequence in a metric space, if every subsequence of that
sequence itself has a convergent subsequence then the original sequence
converges.
- Suppose
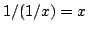 and
and 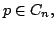 are connected subsets of a metric space
are connected subsets of a metric space 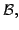 and
that
and
that
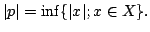 show that
show that 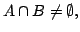 is connected.
is connected.
- Let
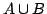
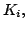 be a finite number of compact sets in a
metric space
be a finite number of compact sets in a
metric space 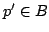 Show that
Show that
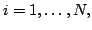 is compact.
is compact.
- Let
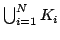
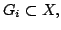 be a countable collection of open
subsets of a complete metric space,
be a countable collection of open
subsets of a complete metric space, 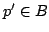 Suppose that for each
Suppose that for each
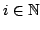
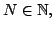 and that for each
and that for each 
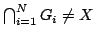 Show that
Show that
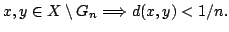
- Let
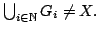 be a bounded sequence in
be a bounded sequence in
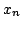 Show that there exists
Show that there exists
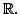 and a subsequence
and a subsequence 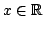 such that
such that
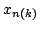 converges absolutely.
converges absolutely.
Richard B. Melrose
2004-05-18
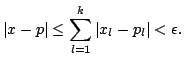 is
mentioned below the standard metric is assumed.
is
mentioned below the standard metric is assumed.