Problem 2

Consider the metric space which is the subset 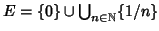$E=\{0\}\cup\bigcup_{n\in\mathbb{N}}\{1/n\}$ of the real numbers with the metric induced by the usual metric on $\mathbb{R}.$

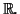
1. What is the set 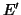$E'$ of limit points of 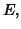$E,$ in $\mathbb{R}$?
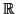2. Describe all the closed subsets of $E.$
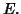
3. Describe all the compact subsets of $E.$
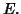
4. Describe all the connected subsets of $E.$

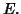
In each case justify your answer.

Proof. [Solution]

1. 0 is the only limit point. It is a limit point since $1/n\to0$ as $n\to\infty$ and all other points are isolated, so cannot be limit points.
2. A subset $C\subset E$ is closed if it is finite or contains 0 (or both). To see this, recall that $C$ is closed in $E$ if and only if it contains all its limit points. A limit point of $C$ must be a limit point of $E$ so the only possibilities are that $C$ has no limit points or it contains $0.$ In the latter case it is closed and the former means that 0 is either not in $C$ and is not a limit point of $C,$ which therefore must be finite.
3. Since $E$ contains its only limit point in $\mathbb{R}$ it is closed and bounded in $\mathbb{R},$ so it is compact by the Heine-Borel Theorem. Thus the compact subsets of $E$ are just the closed sets as described above, since as shown in class a subset of a compact space is compact if and only if it is closed.
4. Let $G\subset E$ be a connected set. If $p=1/n\in G$ is one of the isolated points of $E$ then $G=A\cup B,$ $A=\{p\},$ $B=G\setminus\{p\}$ is a decomposition with $\bar A=A$ and $p\notin\bar B$ so $\bar A\cap B=\emptyset$ and $\bar A\cap B=\emptyset.$ Thus $B=\emptyset$ by the definition of connectedness and $G=\{p\}.$ Thus the only possibility is that $G$ consists of any one point of $E$ and these sets are trivially connected since in any decompostion $\{q\}=A\cup B$ with $A\cup B=\emptyset$ one of $A$ or $B$ must be empty.

$\qedsymbol$