18.02 Practice Problems for Final

The following are a selection of problems whose solutions are in the Notes; after each group of problems is the page number (S.xx) of their solutions. You can pick the topics you feel you need most review on.

I would suggest reviewing by looking first at the four hour exams, and the practice hour exams--redo those problems, paying attention to the ones you originally missed. You have solutions to all of these. Then use the problems on this sheet for additional practice.

Final Exam: Will have about 20 short problems, covering the term's work evenly except there will be some extra weighting on Stokes' theorem.

1.

Simple vector proofs; using the dot product formula:

$$A \cdot B = \vert A\vert\vert B\vert \cos \theta = a_1b_1 + a_2b_2 + a_3c_3 \, .$$

12.1/53    12.2/43, 62     794/18 (S.1)

2.

Vector cross product: its direction and magnitude and the determinantal formula for it. Equations of lines and planes.

12.3/7, 14, 19 (S.2, 3)     12.4/7, 32, 37 (S.5)

3.

Matrices: matrix multiplication, calculating $\det A$ and $A^{-1}$ for $2 \times 2$ and $3 \times 3$ matrices. Solving $Ax=b$ by using $A^{-1}$ and by Cramer's rue.

A square system $Ax=0$ has a non-trivial solution $\Leftrightarrow \det A=0$.

L.17/18a     L.18/4     L.19/1b, 3a (S.4)

4.

Parametric equations. Finding the velocity, acceleration, unit tangent vector and speed of a motion.

601/40a (S.6)     12.5/11, 39 (S.7)

5.

Tangent plane to $z= f(x,y)$; tangent linear approximation:

$$\delta w \approx f_x \Delta x + f_y \Delta y \, .$$

13.4/39, 57 (S.9)     TA-7/3, 5 (S.10)

6.

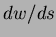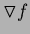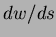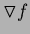Directional derivative $dw/ds$; gradient $\triangledown f$ (including geometric interpretations of its direction and magnitude); deducing approximate values of $dw/ds$ and $\triangledown f$ from map of the level curves of $f(x,y)$.

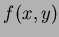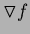$\triangledown f$ is normal vector to contour surfaces of 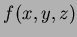$f(x,y,z)$; from this one gets the tangent plane to 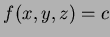$f(x,y,z)=c$. Contour curves.

13.8/12, 23, 32     (S.13)

7.

Chain rule, when variables are independent and when not independent.

13.7/5, 43, 49 (S.12)     N.3/3a, 4 (S.16)

8.

Finding maxima and minima: with and without Lagrange multipliers. Application to line-fitting by method of least squares.

13.5/40, 46 (S.11)     13.9/24 (S.14)    LS/1 (S.13)

9.

Double integrals; putting in limits, changing the order of integration.

I.1/1, 2 (S.19)     14.2/15, 30, 37 (S.20)

10.

Double integrals in polar coordinates.

I.2/5 (S.21)     14.4/2, 16, 23     14.5/33 956/36 (S.22)

11.

Triple integrals in rectangular and cylindrical coordinates.

14.6/5, 33 (S.23)    14.7/9, 12 (S.24)    I.3/11, 12     (I.5)

12.

Spherical coordinates; gravitational attraction.

I.4/14, 16 (I.5)    14.7/26 (S.24)    G.4/3 (S.25)

13.

Line integrals; path independence, conservative fields (in the plane) and exact differentials. Finding the (mathematical) potential function.

15.2/11, 32, 36 (S.26)     Notes 2.7/1, 5, 6 (S.27, 8, 9)

14.

Green's theorem, work form: SP.4/4-C1(b), 4-C4 (S.30)
flux form: Notes 3.4/4 (S.32)     4.5/4a (S.33)

15.

Surface integrals and flux: Notes 9.8/4, 5, 8 (S.36, 37) (Basic surfaces: sphere, cylinder and the graph of $z= f(x,y)$.)

16.

Divergence theorem.

Notes 10.5/5, 6, 8 (S.38, 39)

17.

Line integrals in $3$-space and conservative fields; exact differentials; finding the potential function.

Notes 11.5/1, 4     12.5/2, 3 (S.40, 41)

18.

Stokes' theorem, curl $F$; del operator $\triangledown$, its use in formulas.

SP.7/5-B4 (S.43)     15.7/1, 2 (S.46)