These problems on multiple integration and surface integrals involve a lot of work. Get started early, even though it's not due until next week. Quite a lot of the work is in Part I.
Lecture 27 (Tues. April 13): Triple integrals in rectangular and cylindrical coordinates.
Read: EP, sect. 12.8 to p. 787. Read: SN I, pp. I.2, I.3; Read EP 14.6, pp. 926-929 (concentrate on Exs. 1,2,3); Read EN 14.7, pp. 934-6.
Problems: EP p.791 Probs 5, 9, 11, 15, 23, 25, 27, 55, 60
(give ![]() in terms of
in terms of ![]() ), 61. (Solutions in back of book;
no. 60:
), 61. (Solutions in back of book;
no. 60:
![]() )
More problems: I.3/11, 12, 13
(cylindrical coordinates) (I.5). Even more problems EP: 14.6/1,
5, 33, 39 (
)
More problems: I.3/11, 12, 13
(cylindrical coordinates) (I.5). Even more problems EP: 14.6/1,
5, 33, 39 (![]() only; use symmetry, half the
region), 43 (S.23); 14.7/9, 12 (vol. only),19
(S.24).
only; use symmetry, half the
region), 43 (S.23); 14.7/9, 12 (vol. only),19
(S.24).
Lecture 28 (Thurs. April 15): Triple Integrals in spherical coordinates.
Read: Notes I, p. I.4; EP 14.7, pp. 936-940.
Probs. SN: I.4/14, 16 (I.5); EP 14.7 p.941 21, 26, 29, 40 (S.24,25).
Lecture 29 (Fri. April 16): Gravitational attraction. Vector fields.
Read: SN sect. G, probs: G.3/3, 4 (S.25). Read: SN, Vector Calculus, section 8. Probs. SN 8.2, nos. 1, 3 (8.2).
A rectangular solid has dimensions ![]() . Its density is
. Its density is ![]() .
.
Solution:
![\begin{displaymath}\begin{array}{ll}
\hbox{Inner:} & (x^2 + y^2) z ]^c_0 = c (x^...
...rac{1}{3} b^3 x)]^a_0
= \frac{abc}{3} (a^2+b^2)\, .
\end{array}\end{displaymath}](img11.png) |
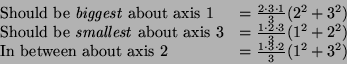 |
Problem: Find volume of the region ![]() bounded above by the spherical
surface
bounded above by the spherical
surface
![]() and below by the paraboloid
and below by the paraboloid ![]() .
.
Solution: Certainly ![]() has circular symmetry. Its projection into the
has circular symmetry. Its projection into the
![]() -plane (its shadow) is a disc of some radius
-plane (its shadow) is a disc of some radius ![]() To determine
To determine ![]() set
set
![]() and solve
and solve
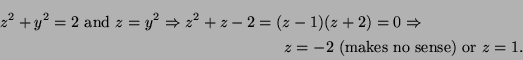
In cylindrical polar coordinates the volume is
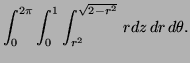 |
![\begin{displaymath}\begin{array}{ll}
\hbox{Inner:} & rz]^{\sqrt{2-r^2}}_{r^2} = ...
...) \quad (\hbox{Book: } \frac{\pi}{6}(8 \sqrt{2}-7))
\end{array}\end{displaymath}](img24.png) |
Definition: The average value of ![]() over a region
over a region
![]() in
in ![]() -space is
-space is
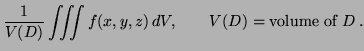
Solution:
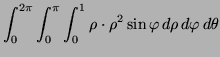 |
Inner:![$\displaystyle \quad \frac{\rho ^4}{4} \sin \varphi ]^1_0 = \frac{\sin \varphi}{4},$](img28.png) Middle: Middle: |
| Answer: |
 |
Inner:![$\displaystyle \quad \frac{1}{4} \left( \frac{\varphi}{2} - \frac{\sin 2 \varphi}{4} \right) ]^{\pi}_0 = \pi/8,$](img35.png) Outer: Outer: |
Answer: |
 |
| Inner: |
|
| Middle: |
| Answer: |
Solution:
Grav. attractions on vertex of solid icream cone with density ![]()
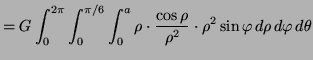 |
Inner:![$\displaystyle \frac{\rho^2}{2} \sin \varphi \cos \varphi ]^a_0 = \frac{a^2}{2} \sin \varphi \cos \varphi$](img50.png) |
|
Middle:![$\displaystyle \frac{a^2}{4} \sin^2 \varphi ]^{\pi/6} = \frac{a^2}{4} \cdot \frac{1}{4} \quad = \frac{a^2}{16}$](img51.png) |
|
Outer: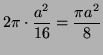 |
Answer: |
Solution: Put the hemisphere with its flat surface up and its pole at the origin. Then do the integral in two pieces: the inner solid cone and the outer shell.
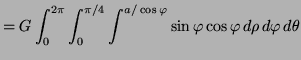
(Drop ![]() during the integration)
during the integration)
Evaluating Cone part:
| Inner: |
|
Middle:![$\displaystyle - a ar \varphi ]^{2 \pi/4} = a\left(1- \frac{\sqrt{2}}{2}\right),$](img59.png) |
|
Outer: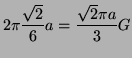 |
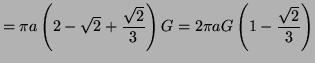 |
(The field is tangent to a circle centered on the ![]() -axis, lying
in a plane perpendicular to the
-axis, lying
in a plane perpendicular to the ![]() -axis, with direction given by
the right hand rule, and magnitude inversely proportional to the
distance from the
-axis, with direction given by
the right hand rule, and magnitude inversely proportional to the
distance from the ![]() -axis.)
-axis.)
Solution: