Part I: (10 pts)
Lecture 22. (Thurs. April 1): Differentials, exactness. Criterion for conservative fields; finding potential functions. Read: Notes pp. 2.1-2.5 (p. 2.6 is optional--it is covered in 18.03). EP pp. 980-982 covers about the same material; if you read the book, be sure to read the Notes p. 2.1 for the proof of the theorem, which the book omits. Problems: Work: Notes 2.7 5a (use method 1 of notes), 5b (use method 2), 6ab (do it using both methods) (S. 28)
If
![]() , then
, then ![]() is called the (mathematical)
potential function. The physical potential function is given by
is called the (mathematical)
potential function. The physical potential function is given by
![]() , so in physics classes the relation is written
, so in physics classes the relation is written
![]() .
.
Lecture 23. (Fri. April 2): Green's Theorem. Read EP, pp. 986-989. Probs: Notes: SP.4/4-C1, a, b, c, SP.5/4-C2, 3, 4, 5 (S.30)
Lecture 24. (Tues. April 6): Two-dimensional flux. Normal form of Green's Theorem. Read: Notes secs. 3 and 4; EP pp. 989-992 is similar, but more condensed; the normal form is called the ``vector form'' of Green's theorem. Probs: Notes: 3.4/lac,2 (give brief reason or draw picture) 3.4/3, 4, 5 (give a direct calculation; don't use Green) 4.5/4b (S. 31-33)
Lecture 25 (Thurs. April 8): Extensions and applications of Green's Theorem; topology in the plane. Read: Notes: 5 and 6.
Exam 3. (Fri. April 9) 2:05-2:55 in Walker. This will cover double integrals and line integrals through Lecture 24. (Lecture 25 will not be included.)
Part II
Solution:
Solution:
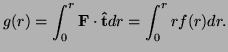 |
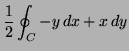 |
|||
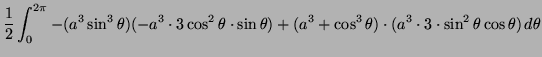 |
|||
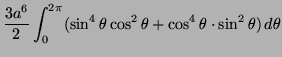 |
|||
 |
|||
 |
|||
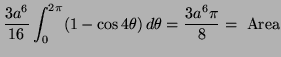 |
Find the closed curve ![]() in the plane for which
in the plane for which
![]() has the biggest value, and determine this
biggest value. (Use Green's theorem, and study the resulting
double integral - how would you make it biggest?)
has the biggest value, and determine this
biggest value. (Use Green's theorem, and study the resulting
double integral - how would you make it biggest?)
Solution: By Green's theorem
![$\displaystyle \oint x^2ydx+x(1-y^2)dy=\iint_R[(1-^2)-x^2]dA=\iint_R(1-x^2-y^2)$](img36.png) |
Find the flux of the vector field
![]() through the
square of side two with center at the origin and one vertex at
through the
square of side two with center at the origin and one vertex at
![]() .
.
Solution: With ![]() this square and
this square and ![]() its boundary,
its boundary,
![]()
Solution:
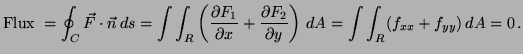 |
These one should be saved for next week, they were not supposed to be on this problem set.
A regular solid has dimensions ![]() . Its density is
. Its density is ![]() .
.
Find the average distance of a point in a solid sphere of radius
![]() from
from
Definition: The average value of ![]() over
region
over
region ![]() in
in ![]() -space is
-space is
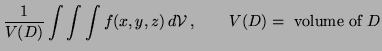
For (c), you have to choose whether to make the limits easy, but
the integrand hard, or to place the sphere so the integrand is
easy, but the limits harder. Do the latter: place the sphere so
the point is at the origin and the axis along the ![]() -axis; this
makes the integrand easy and the main issue is the equation of the sphere.
-axis; this
makes the integrand easy and the main issue is the equation of the sphere.