18.02 Problem Set 7 (due Friday April 2, 1:45PM, 2-106)

Part I:

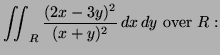
Hand in the underlined problems; the others are for practice.

Lecture 19. Thurs. (March 18): Changing variables in a double integral. Read SN sect CV, supplementing with Examples 1-4 in EP sect 14.9.

Problems: EP page 955 no. 9, page 956 no. 13, SN sect. Vect Calc, page 2.7 1, Special Problem: The original problem was to evaluate

$$\iint_R \frac{(2x-3y)^2}{(x+y)^2} \, dx \, dy \hbox{~over~} R:$$

where $R$ is the region to the right of the $y$-axis, below the $x$-axis and above the line $2x-3y=4.$ However this integral is undefined as a Riemann integral (because the integrand is unbounded) or, more sensibly is $+\infty$ as a Lebesgue integral (or as an improper Riemann integral). In short I should have been more careful when I copied this problem, it is bad, bad bad! The difficult is that the line $x+y=0$ where the integrand is infinite is inside the domain $R.$ If instead I had asked you to evaluate

$$\iint_R \frac{(2x-3y)^2}{(x+y+3)^2} \, dx \, dy$$

for the same $R$ we would have had less trouble!

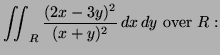
Solutions: EP page 955, no. 9: For $u=xy,$ $v=xy^3$ the Jacobian is

$$\frac{\partial(u,v)}{\partial(x,y)}=\left\vert\begin{matrix} y&x\\ y^3&3xy^2\end{matrix}\right\vert=2xy^3.$$

Thus $\frac{\partial(x,y)}{\partial(u,v)}=1/2v.$ The area integral is therefore

$$\int_3^6\int_2^4 \frac{du\,dv}{2v}=\int_3^6\frac{dv}{2v}=\ln2.$$

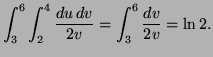
EP page 956, no. 13: Since $x=3r\cos\theta$ and $y=2r\sin\theta,$ the Jacobian is

$$\frac{\partial(x,y)}{\partial(r,\theta )}=\left\vert\begin{matrix... ...theta &-3r\sin\theta \\ 2\sin\theta &2r\cos\theta \end{matrix}\right\vert=6r.$$

The integral for the volume is

$$\begin{multline*} \int\int_R(x^2+y^2)6rdr\,d\theta =\int_0^{2\pi}\int_0^16r^3(4+... ... =\int_0^{2\pi}\frac32(4+5\cos^2\theta )d\theta =\frac{39\pi}2. \end{multline*}$$

Special Problem: Make the change of variables $v=2x-3y,$ $u=x+y.$ The Jacobian is

$$\frac{\partial(u,v)}{\partial(x,y)}= \left\vert\begin{matrix}1&1\\ 2&-3\end{matrix}\right\vert=-5.$$

In terms of $u$ and $v$ the region of integration is between $v=0$ and $v=4$ and when $v=2x-3y$ is fixed, $u$ runs from $x=0,$ where it is $y=-v/3,$ to $y=0$ where it is $x=v/2.$ I leave it as an excercise to evaluate the resulting iterated integral

$$\int_0^4\int_{-v/3}^{v/2}\frac{v^2}{(u+3)^2}\frac{du\,dv}5.$$

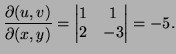
Lecture 20. Fri. (March 19): Vector fields. Line integrals in the plane.

Read SN sect. on Vect. Calc. section 1 (covered also in EP 15.1, pp. 960-1). Probs. SN Vect. Calc. Exercises 1.1, nos. 3i, ii, iii, 4 (solns p. 1.5). Read EP 15.2 pp. 969-74. Probs. EP page 976, 6, 9, 33a, b, 34, 35, 36 (S.26).

Lecture 21. Tues. (March 29): Path independence; conservative fields in the plane. Read 15.3 to p. 979. Problem: Work SN Vect. Calc. page 2.7 1, 2, 3 (S.27) However, the solution to Problem 3 on page S.27 is incorrect. Rather, ${\bf F}={\bf\nabla} f=\cos x\cos y{\bf i}-\sin x\sin y{\bf j}.$ The rest is correct.

Remark: The Fundamental Theorem of Calculus for line integrals is Theorem 1. You should be able to state and prove the theorem (in the plane; ignore $z$). The book writes $\int_C {\bf F}\cdot{\bf T}\, ds$, in the lectures and notes we use $\int_C{\bf F}\cdot {\bf dr}$. Both have the same meaning: the line integral which calculates the work done by the field ${\bf F}$ carrying a unit test object along the curve $C$.

Part II: (15 pt)

Directions: Try each problem alone for 15 minutes. If you subsequently collaborate, this should be acknowledged and solutions must be written up independently.

Problem 1. (Thurs. 5 pt) Work EP page 958 (Misc. Problems) no. 52.

Solution: The integral is

$$I=\int\int_R\exp\big(\frac{x-y}{x+y}\big)dx\,dy.$$

For the suggested change of variables, $u=x-y,$ $v=x+y$ the Jacobian is

$$\frac{\partial(u,v)}{\partial(x,y)}= \left\vert\begin{matrix}1 & -1\\ 1&1\end{matrix}\right\vert=2.$$

Thus $dx\,dy=\frac12du\,dv$ The region of integration, $R,$ is the set where $x,y\ge0$ and $x+y\le1.$ In terms of the new variables this is $0\le v\le 1,$ $u+v\ge0,$ $u-v\ge0.$ Thus

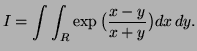
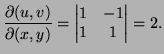
$$I=\frac12\int_{0}^1\int_{-v}^v \exp(u/v) du\,dv=\frac12\int_0^1 \big[v\exp(u/v)\big]^{v}_{-v}=\frac12\int_0^1v(e-\frac1e)=\frac14(e-\frac1e).$$

Problem 2. (Fri. 2 pt) Write down the velocity field for a standard $2$-dimensional flow between the lines $x=0$ and $x=1$: The flow is upwards, with parabolic cross-section; i.e., along any horizontal line segment between 0 and $1$, the velocity vector has magnitude 0 at the two ends, while in between its length increases and decreases so the tips of the vectors lie on a parabola, whose maximum height is $1$, in the middle. Indicate reasoning. (This is the way a liquid flows in a pipe if it adheres to the pipe walls.)

Solution: The direction of the vector field is always ${\bf j}.$ Its magnitude must be $\vert{\bf F}\vert=4x(1-x),$ since it has to be quadratic and vanish at $x=0$ and $x=1$ and have size $1$ when $x=\frac12.$ Thus

$${\bf F}=4x(1-x){\bf j}.$$

Problem 3. (Fri. 3 pt) Imagine the $z$-axis represents an infinitely long, uniformly charged wire. The electric force it exerts on a unit charge at the point $(x,y)$ is given by

$$F(x,y) = k(x{\bf i} + y{\bf j})/(x^2 + y^2) \, .$$

Find by direct calculation of the line integral in each case the work done by the force in moving a unit charge along the paths:

1.

line from $(0,1)$ to $(\infty ,1)$.

2.

circle of radius $a$ with center at origin, traced counterclockwise.

3.

line from $(1,0)$ to $(0,1)$ (use integral tables in the book covers).

Solution:

The vector field is

$${\bf F}=\frac{kx{\bf i}+ky{\bf j}}{x^2+y^2}$$

so the work done along a curve $C$ is

$$k\int_C\frac{xdx+ydy}{x^2+y^2}.$$

1.

The curve is $x$ running from 0 to $\infty$ while $y=1.$ Thus the work done is

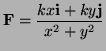
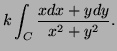
$$k\int_0^\infty \frac{xdx}{x^2+1}=\frac k2\ln(x^2+1)\big]^\infty_0=\infty.$$

So an infinite amount of work must be done (just like 18.02!)

2.

The curve is $x=a\cos t,$ $y=a\sin t,$ $t$ running from 0 to $\pi/2.$ Thus $dx=-a\sin t dt,$ $dy=a\cos t dt$ and the work done is

$$k\int_0^{\pi/4} \frac{-a^2\cos t\sin t+a^2\sin t\cos t}{a^2}dt=0.$$

3.

Parameterize by $y=1-x,$ $dy=-dx,$ $x$ running from $1$ to $0,$ so the work done is

$$k\int_1^0\frac{xdx+(1-x)(-dx)}{x^2+(1-x)^2}=\int_1^0\frac{(2x-1)dx}{2x^2-2x+1}= \frac12\ln(2x^2-2x+1)\big]^0_1=0.$$

Problem 4. (Fri. 8 pt) Answer the same questions as in SN Vect. Calc. page 2.7 no. 1 for the function $f(x,y)=xy(x+y)$, and the path $C$ given by the quarter circle running from $(0,1)$ to $(-1,0)$.

Solution:

a)

Since $f=x^2y+xy^2,$ ${\bf F}=(2xy+y^2){\bf i}+(x^2+2xy){\bf j}.$

b)

Directly: Parameterize the curve by $x=\cos t,$ $y=\sin t,$ $\pi/2\le t\le \pi.$ Thus $dx=-\sin t dt,$ $dy=\cos tdt$ so the line integral is

$$\int_{\pi/2}^{\pi} (-\sin^3t-2\cos t\sin^2t+\cos^3t+2\sin t\cos^2t)dt.$$

Using the formulæ $\sin^3t=\sin t(1-\cos^2t)$ and $\cos^3t=\cos t(1-\sin^2t)$ the integral becomes

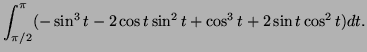
$$\int_{\pi/2}^{\pi} (-\sin t-3\cos t\sin^2t+\cos t+3\sin t\cos^2t)dt =\cos t-\sin^3t-\sin t-\cos^3 t\big]^{\pi}_{\pi/2}=0.$$

A simpler path between these two point is down the y-axis to the origin and then along the x-axis. The integrand vanishes on both pieces so the integral is zero. By the fundamental theorem

$$\int_C {\bf F}\cdot d{\bf r}=f(x,y)\big]^{(0,1)}_{(-1,0)}=0.$$