Part I:
Hand in the underlined problems; the others are for practice.
Lecture 16. Thurs. (March 11): Double and iterated
integrals in rectangular coordinates.
Read EP 14.1-14.3. Concentrate on:
Lecture 18. Tues. (March 16): Double integrals in polar coordinates; applications.
Problem 1. (Thurs. 3 pt) A rectangular prism is made by taking a long piece of wood with a rectangular cross-section, sawing off one end perpendicularly, and the other end at an arbitrary angle (so that the four edges have in general four different lengths). Show by double integration that
volume of prism ![]() (cross-sectional area)
(cross-sectional area) ![]() (average of
the four lengths).
(average of
the four lengths).
[Place the prism as shown in the picture, and take ![]() as
the equation of the top surface.]
Oops, fogot the picture. Oh well I hope is was reasonably clear anyway.
as
the equation of the top surface.]
Oops, fogot the picture. Oh well I hope is was reasonably clear anyway.
This formula can be thought of as generalizing the formula for the area of a trapezoid.
Solution: If the prism is placed as suggested, with sides in the three
coordinate planes and sloping end of the form ![]() then the volume
of the prism is the integral over the rectangular region
then the volume
of the prism is the integral over the rectangular region ![]() of the
xy-plane where
of the
xy-plane where
![]()
![]() of
of
![]()
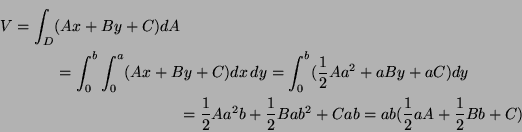
Problem 2. (Tues. 3 pt) Work Problem 32 EP page 901.
Solution: Change the order of integration - the region is a triangle and
![$\displaystyle \int_0^{\sqrt\pi}\int_y^{\sqrt\pi}\sin x^2 dx\,dy= \int_0^{\sqrt\...
... x^2 dy\,dx= \int_0^{\sqrt\pi} x\sin x^2 dx= [-\frac12\cos x^2]_0^{\sqrt\pi}=1.$](img14.png) |
Problem 3. (Tues. 3 pt)
A split log has a semi-circular cross-section, and a radius ![]() .
A
.
A ![]() wedge-shaped piece is cut out of it. What is the
volume of the piece? ( Hint: Calculate half the
volume of something else.)
wedge-shaped piece is cut out of it. What is the
volume of the piece? ( Hint: Calculate half the
volume of something else.)
Solution: There is likely to be much confusion about this one, because I
did not add a picture. Give full marks for any reasonable interpretation. I
meant that the top surface of the log was
![]() and it lies in
and it lies in
![]() stretching in the y-direction. The prism was supposed to be
stretching in the y-direction. The prism was supposed to be
![]() in the xy-plane, in
in the xy-plane, in ![]() - so between the lines
- so between the lines ![]() and
and
![]() The volume is therefore twice the integral over
The volume is therefore twice the integral over
![]()
![]() of
of
![]() i.e.
i.e.
![$\displaystyle \int_0^a\int_0^x\sqrt{a^2-x^2} dy\,dx= \int_0^ax\sqrt{a^2-x^2}dx=-\frac13(a^2-x^2)^{\frac3/2}\big]^a_0=a^3/3.$](img24.png) |
As I say, interpretation may differ on this one!
Problem 4. (Tues. 3 pt) Work Problem 18, EP page 913.
Solution: Change to polar coordinates, the main problem is to find the
limits of integration. The region is
![]() restricted
by
restricted
by
![]() The condition
The condition
![]() means
means
![]() This is the circular region with center
This is the circular region with center ![]() and radius
and radius ![]() Thus the
region of integration is a quarter of this disk - the upper right
quarter. So the whole integral becomes, in polar coordinates
Thus the
region of integration is a quarter of this disk - the upper right
quarter. So the whole integral becomes, in polar coordinates
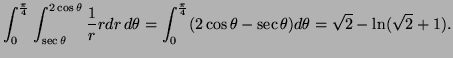 |
Problem 5. (Tues. 3 pt)
Find the centroid (center of gravity) of the plane lamina lying
between the parabolas ![]() and
and ![]() , if the density
function is
, if the density
function is
![]() .
.
Solution: By symmetry the centroid must lie on the x-axis, so we only need
to compute ![]() - we can compute this for the upper half, since it
will have the same
- we can compute this for the upper half, since it
will have the same ![]() We can set
We can set ![]() since it will cancel, thus
since it will cancel, thus
Mass |
![$\displaystyle \int_0^1\int_{y^2}^{2-y^2}x^2 dx\,dy=\int_0^1\frac13[8-12y^2+6y^4-2y^6] dy =\frac13[4+\frac{32}{35}].$](img40.png) |
Problem 6. (Tues. 3 pt)
Find the moment of inertia of a thin circular plate of radius ![]() and density
and density ![]() about
about
(Hint: In both cases place the point at the origin and
place the circle so a diameter lies along the ![]() -axis. Use
polar coordinates. There are integral tables in the front and
back cover of your book which use can use.)
-axis. Use
polar coordinates. There are integral tables in the front and
back cover of your book which use can use.)
Solution:
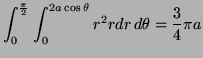 |
 |