18.02, Problem set V. Due March 11, 12:45 in 2-106

Part I(10 pts)

Hand in the underlined problems only; the others are for more practice; one point each for a correct solution.

Lect 10 (Feb 26) Read: EP Sect 13.6 pages 837-8, Sect 13.7 to page 846. SN TA, pp 3-7. Probs: EN page 843 1, 6, 18; page 844 36. EN page 853, nos 2, 5, 8, 36.

Lect 11 (Feb 27) Read EN 13.7 pages 846-7, Sect 13.8. Probs. EN page 854 nos. 43, 49; page 863, nos. 2, 10, 12, 23, 32.

Lect 12 (Mar 2) Read EN 13.9 (after top of page 870 is optional). Probs EN page 872 no 24, page 873 nos 42, 46.

Lect 13 (Mar 4) EN 13.10, SN P. Read EN Sect 13.10. Read SN P. Probs EN page 881 nos 4, 6, 7, 8, p. 882 no. 32.

Lect 14 (Mar 5) Read SN Sect N, Probs SN Sect N, 1, 2, 3, 4, 5a, 6

Part II (25 pts)

Directions Try each problem alone for 20 minutes; if you collaborate later, solutions must be written up independently; no consulting old problem sets.

1.

(3 pts)

Find the point $(x,y)$ in the plane for which the sum of the squares of its distances from the three points $(a_i, b_i) \, , i=1,2,3$, is a minimum.

Give a physical interpretation of your answer.

(Use summation notation; in this way your work will apply to any number of points.)

Solution: The sum of the squares of the distances from $(x,y)$ is

$$S=\sum\limits_{i=1}^3 \left((x-a_i)^2+(y-b_i)^2\right)$$

Since

$$\partial S/\partial x=2\sum\limits_{i=1}^3(x-a_i),\ \partial S/\partial x=2\sum\limits_{i=1}^3(y-b_i)$$

the only critical point is at

$$x=\frac13\sum\limits_{i=1}^3a_i,\ y=\frac13\sum\limits_{i=1}^3b_i.$$

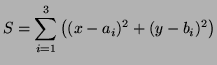
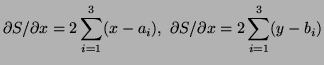
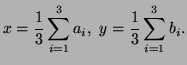
This point is the `center of gravity' or `center of mass' for particles of unit mass at the three points.

2.

(4 pts)

What is the maximum possible volume of a rectangular box inscribed in a hemisphere of radius $a$? (You may assume that one face of the box lies in the planar base of the hemisphere. For each calculation, use as variables not the lengths of the sides of the base, but rather half the lengths.)

Solution: If $x$ and $y$ are half the side lengths and $z$ is the height then we can assume that $x^2+y^2+z^2=a^2.$ The volume is $4xyz$ so we can maximize $w=xy(a^2-x^2-y^2)^{\frac12}.$ Then

$$\partial w/\partial x=y(a^2-2x^2-y^2)(a^2-x^2-y^2)^{-\frac12}.$$

Since $y\not=0$ at maximum, $a^2=2x^2+y^2.$ Similarly from the $y$-derivative, $a^2=x^2+2y^2,$ so $x=y=a/{\sqrt3}$ (since both are positive). Thus the maximum volume is $4a^3/3\sqrt3.$

3.

(3 pts)

Find the line which best fits the three data points $(-1, -1)$, $(0, 1)$, $(2,1)$, in the sense of least-squares approximation.

(Don't use any formulas; do the work from scratch, as a max-min problem, using the definition of least-squares approximation. Differentiate the squares directly using the chain rule; don't multiply them out first (see the notes LS).)

Solution: If the line is $y=mx+b$ then we must minimize

$$D=(-m+b+1)^2+(b-1)^2+(2m+b-1)^2.$$

Calculating directly, $\partial D/\partial m=10m+2b-6$ and $\partial D/\partial b=2m+6b-2$ so the line is

$$y=\frac47x+\frac17.$$

4.

(2 pts)

Prove that the tangent planes to points on the surface $xyz=k$ ($k>0$ a constant) in the first octant cut out of the first octant a tetrhedron of constant volume.

5.

(4 pts)

Notes: LS/5. Let $x=(x_1, \ldots, x_n)$, $y=(y_1, \ldots, y_n)$, $1=(1, \ldots, 1)$, etc.

Express your answer to this problem in the form of a matrix equation $Aa=r$, where $a=(a,b,c)'$ and the matrix $A$ has as its entries various scalar products of the above vectors.

Solution: In matrix form the solution looks like

$$\left[{ \begin{array}{ccc} n & x\cdot 1 & y\cdot1\\ x\cdot1... ...array}{c} 1\cdot z\\ x\cdot z \\ y\cdot z\end{array}}\right]$$

6.

(5 pts)

Work out and classify the critical points of $3x^2 + 6xy+2y^3+12x-24y$. (Use the second-derivative test and give the $(x,y)$-coordinates of the points.)

Solution: If $w=3x^2 + 6xy+2y^3+12x-24y$ then $\partial w/\partial x=6x+6y+12$ and $\partial w/\partial y=6x+6y^2-24.$ So the coordinates of the critical points satisfy $x+y=-2$ and $x+y^2=4.$ This gives $y^2-y-6=(y+2)(y-3)=0$ so the critical points are $(0,-2)$ and $(-5,3).$ To determine the type of critical points compute the second derivatives:

$$w_{xx}=6,\ w_{xy}=6,\ w_{yy}=12y.$$

So $w_{xx}w_{yy}-w_{xy}^2=72y-36=36(2y-1)$ is negative at $(0,-2)$ which is therefore a saddle and positive at $(-5,3)$ which is a minumum, since $w_{xx}>0.$

7.

(4 pts) Let $f(x,y)$ be the square of the distance from the point $(0,0,2)$ to the point $(x,y,z)$ on the saddle-shaped surface $z=xy.$ Find the critical points of $f(x,y),$ classify them and then tell what the minimum distance is and for which point (or points) it is achieved.