


Next: About this document ...
18.02 Problem Set 4 (due Friday 2/26, at 1:45 in 2-106)
Part I
Hand in the underlined problems only; the others are
for more practice. (After each set of problems is given in the
Solution page where they are solved.)
Lecture 7. Thurs. Feb 18 Functions, partial derivatives, tangent plane:
Read EP 13.2, 13.4, SN TA-1,2. Probls EP p.805-807, nos. 7, 15;
24, 25, 53-58 p. 822-3
nos. 4, 6, 12, 21, 39, 40,
57 solns SN (S.9)
Lecture 8. Tues. Feb 23 Maximum-minimum problems. Least squares approximation.
Read EP 13.5, SN LS. probs EP p. 834 nos 32, 40,
46 solns SN (S.11) prob. LS-3 no. 1
Part II
Directions: Try each problem alone separately for
20 minutes. If you subsequently collaborate, solutions must be
written up independently. It is illegal to consult problem sets
from previous years or to copy directly from anyone else.
Problem 1. (Thurs. 4 pts.)
Let 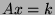 be a system of linear equations, where
be a system of linear equations, where 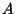 is a
nonsingular matrix:
is a
nonsingular matrix:
Let
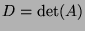 . Since
. Since 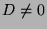 , the system has a unique
solution
, the system has a unique
solution
![$[x_0,y_0,z_0]$](img6.png) , which depends on the matrix
, which depends on the matrix 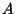 and the
vector
and the
vector 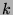 . Thus
. Thus 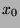 is a function of the
is a function of the  variables
variables
 . Calculate
. Calculate
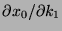 and
and
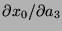 , expressing your answer compactly
in terms of
, expressing your answer compactly
in terms of  , and as few of the
, and as few of the  variables as
possible.
variables as
possible.
(Hint: Use Cramer's rule and the Laplace expansion by cofactors.)
Solution: By Cramer's rule, 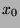 is the quotient of two determinants
is the quotient of two determinants
We may expand the top determinant along the first row and conclude that it
is a linear function of  Thus
Thus
Both top and bottom determinants depend on 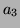 so we need to expand both
along the top row and use the chain rule to see that
so we need to expand both
along the top row and use the chain rule to see that
Expanding out the 2x2 determinants to get an explicit formula is a good
idea, but we take no marks off if it is not done.
Problem 2. (Thurs. 5 pts; 2, 3)
The surface of 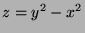 , though curved, can be thought of of
as made up entirely of lines.
, though curved, can be thought of of
as made up entirely of lines.
- 1.
- Find the equation of the tangent place at the point
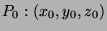 on the surface.
on the surface.
- 2.
- Show that if
 ,
, 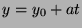 ,
, 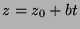 is a
general line through
is a
general line through 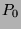 , it is possible to choose
, it is possible to choose  and
and
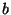 in two different ways so that the two corresponding lines lie
both in the tangent plane and in the surface.
in two different ways so that the two corresponding lines lie
both in the tangent plane and in the surface.
Solution:
- 1.
- The surface is
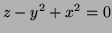 so its tangent plane at
so its tangent plane at
 is
is
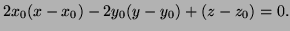
- 2.
- To lie in the tangent plane we must have
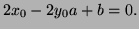 To lie on
the surface we must have
To lie on
the surface we must have
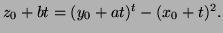 Expanding out this
means
Expanding out this
means
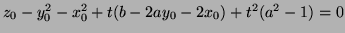 for all
for all  So all
three coefficients must vanish. Now,
So all
three coefficients must vanish. Now,
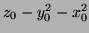 since the point is
on the surface. The vanishing of
since the point is
on the surface. The vanishing of
 means the line is tangent
to the surface (so in the tangent plane) and determines
means the line is tangent
to the surface (so in the tangent plane) and determines 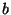 from
from 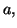
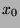 and
and 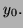 The third condition
The third condition  has
two solutions
has
two solutions 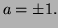 So there are two lines of this form in the surface
through each point, namely
So there are two lines of this form in the surface
through each point, namely 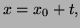


Problem 3. (Thurs. 2 pts)
Show
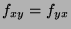 if
if
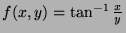 .
.
Problem 4. (Thurs. 3 pts)
Laplace's equation is
 .
.
- 1.
- Verify that
 satisfies the equation.
satisfies the equation.
- 2.
- Find all functions
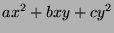 (
( ,
, 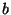 ,
, 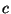 constants) that satisfy Laplace's equation, and show they can
all be written as
constants) that satisfy Laplace's equation, and show they can
all be written as
 , where
, where 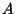 and
and  are
arbitrary constants, and
are
arbitrary constants, and 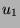 and
and  are particular
functions of the given form.
are particular
functions of the given form.
- 3.
- Answer the same question as in (b) for
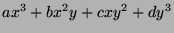 .
.
- 1.
- Verify that
 satisfies the equation.
satisfies the equation.
- 2.
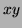 satisfies the equation as does
satisfies the equation as does  but
but 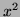 does not. It
follows (by directly differentiating) that the solutions are
does not. It
follows (by directly differentiating) that the solutions are
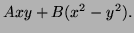
- 3.
- Answer the same question as in (b) for
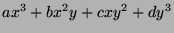 .
Differentiating direclyt give
.
Differentiating direclyt give
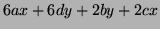 so that the ones that
satisfy Laplace's equation must have
so that the ones that
satisfy Laplace's equation must have 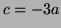 and
and 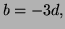 they are
they are
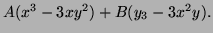



Next: About this document ...
Richard B. Melrose
1999-03-01
![]() be a system of linear equations, where
be a system of linear equations, where ![]() is a
nonsingular matrix:
is a
nonsingular matrix:
![$\displaystyle A=\left[\begin{matrix}a_1 &a_2 &a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3...
...\right] \hbox{ and }
x= \left[\begin{matrix}x\\ y\\ z\end{matrix}\right]\, .
$](img3.png)
![]() is the quotient of two determinants
is the quotient of two determinants

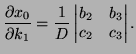
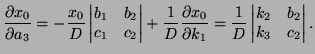
![]() , though curved, can be thought of of
as made up entirely of lines.
, though curved, can be thought of of
as made up entirely of lines.
![]() if
if
![]() .
.
![]() .
.