


Next: About this document ...
18.02 Problem Set 11 (due Friday, May 7, 1999)
Part I (7 points)
Hand in the the underlined problems; the others are for practice.
Lecture 33 (Tues. May 4): Line integrals in space,
 , exactness, potentials.
, exactness, potentials.
Read SN: Sections 11, 12 and p. 15.1; Problems: SN p. 11.5 nos. 1, 2,
4, 5 (S.40) SN p. 12.4 and 12.5 nos 1, 2,
3ab(ii) (both methods), 5 (S. 41-2)
Lecture 34 (Thurs. May 6): Stokes' Theorem.
Read: SN Section 13, EP Section 15.7. Problems: SP.7 nos. 5-B3,
B4, B5, B7 (S. 43-4).
Lecture 35 (Fri. May 7): Stokes' Theorem, cont'd. Applications.
Part II (11 points)
Directions: Try each problem alone for 25 minutes. If
you subsequently collaborate, solutions must be written up
independently. It is illegal to consult old problem sets.
- 1.
-
(Tues. 2 pts)
- (a)
-
For what value(s) of the constant
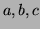 will the field
be conservative?
will the field
be conservative?
- (b)
-
Using these values of the constants, find a potential function
for the field, by either method described in the Notes. (Show
systematic work.)
Solution:
- (a)
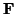 will be conservative if
will be conservative if
 Since
Since

this vanishes (identically) exactly when 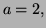
 and
and 
- (b)
- Method 1: Calculate the work integral of
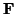 along the curve
which starts at the orgin, goes along the x-axis to
along the curve
which starts at the orgin, goes along the x-axis to 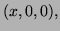 then in the
direction of
then in the
direction of  to
to  then in the z-direction to
then in the z-direction to 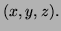
Method 2: Solve 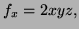 giving
giving
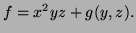 Then substitute in
Then substitute in
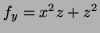 giving
giving 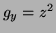 so
so
 and
and
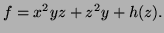 Finally substitute this in
Finally substitute this in
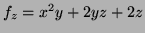 giving
giving 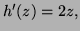 so
so
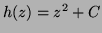 and the general answer is
and the general answer is
 as before.
as before.
- 2.
-
(Thurs. 2 pts)
Suppose that in
 -space,
-space,
 , where the
components of
, where the
components of 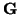 have continuous second partial derivatives. Prove
that, if
have continuous second partial derivatives. Prove
that, if 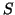 is a closed surface, then
in two ways:
is a closed surface, then
in two ways:
- (a)
-
by the divergence theorem;
- (b)
-
by drawing a closed curve
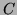 dividing
dividing 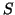 into two parts and
applying Stokes' theorem to each.
into two parts and
applying Stokes' theorem to each.
Solution:
- (a)
- By the divergence theorem,
Since
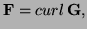

by the equality of mixed second derivatives.
- (b)
- Choose a closed curve
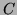 which divides
which divides 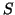 into two parts (such as a
little circular curve). Let
into two parts (such as a
little circular curve). Let 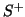 be the half with outward normal which has
the correct orientation for Stokes' theorem. Then the other half,
be the half with outward normal which has
the correct orientation for Stokes' theorem. Then the other half, 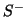 with outward normal has the correct orientation for
with outward normal has the correct orientation for  which is
which is 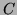 run
backwards. Applying Stokes' theorem twice
run
backwards. Applying Stokes' theorem twice
with both 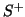 and
and 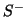 having the outward orientation of
having the outward orientation of 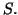 Since
Since
it follows
that
- 3.
- (Thurs, 3 pts) Which of the following differentials are exact? For
each one which is, express it in the form
 for a suitable function
for a suitable function
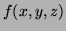 .
.
- (a)
-

- (b)
-

- (c)
-
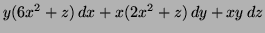
Solution - in each case compute 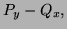
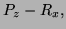

- (a)
- Exact, it is
 for
for

- (b)
- Exact, it is
 for
for 
- (c)
- Exact, it is
 for
for
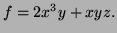
- 4.
- (Thurs 1 pt) Find
 , if
, if
 .
.
Solution: From the formula above,
- 5.
- (Thurs, 2 pts) The fields
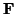 below are defined for all
below are defined for all 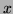 ,
,  ,
,
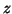 . For each,
. For each,
- (a)
- Show that curl
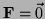 .
.
- (b)
- Find a potential function
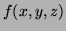 . Use either
method, or inspection.
. Use either
method, or inspection.
- i.
-
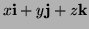
- ii.
-
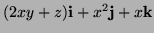
- iii.
-

Solution -
- (a)
-

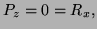
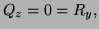 so
so
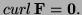
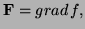
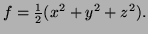
- (b)
-
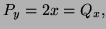

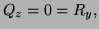 so
so
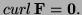
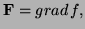
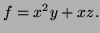
- (c)
-

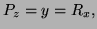
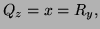 so
so
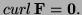
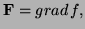
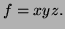



Next: About this document ...
Richard B. Melrose
1999-05-07
![]() , exactness, potentials.
, exactness, potentials.

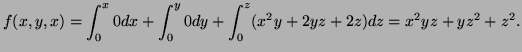
![]() giving
giving
![]() Then substitute in
Then substitute in
![]() giving
giving ![]() so
so
![]() and
and
![]() Finally substitute this in
Finally substitute this in
![]() giving
giving ![]() so
so
![]() and the general answer is
and the general answer is
![]() as before.
as before.

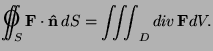

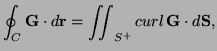
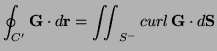

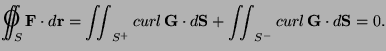
![]()
![]()
![]()