Let ![]() be the disc having this circle as its boundary;
be the disc having this circle as its boundary; ![]() the
spherical cap forming the upper surface, and
the
spherical cap forming the upper surface, and ![]() the cone forming
the lower surface. Orient all three surfaces so that the normal
vector points generally upward (i.e, has a positive
the cone forming
the lower surface. Orient all three surfaces so that the normal
vector points generally upward (i.e, has a positive
![]() -component).
-component).
Calculate the flux of the vector field
![]() over each of these
three surfaces. In each case, do the calculation directly from
the definition of the surface integral for flux, as in the Notes
and Part I problems.
over each of these
three surfaces. In each case, do the calculation directly from
the definition of the surface integral for flux, as in the Notes
and Part I problems.
Solution.
Flux through ![]()
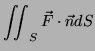 |
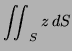 |
||
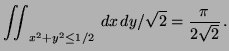 |
Since
Flux through ![]()
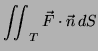 |
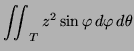 |
||
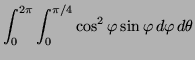 |
|||
Flux through ![]() On
On ![]()

For what radius ![]() will the heat flow across the sphere be
greatest?
will the heat flow across the sphere be
greatest?
Solution: The heat flow across a surface is the flux of the vector field
![]() where
where ![]() is the temerature distribution. In this case,
is the temerature distribution. In this case,
Thus the flux across the sphere of radius
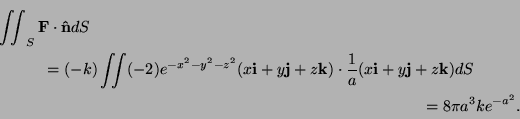
The correct value for the flux over the disc ![]() is
is
![]() . Using this:
. Using this:
- (a)
-
Use the divergence theorem (and the formula for the volume of a
solid cone) to get the flux over the conical surface
 .
(Watch for orientations!)
.
(Watch for orientations!)
- (b)
-
Similarly, use the divergence theorem to get the flux over
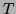 . (get the volume of the whole ice cream cone and subtract
the cone volume to get the volume of the spherical cap on top.)
. (get the volume of the whole ice cream cone and subtract
the cone volume to get the volume of the spherical cap on top.)
Solution:
- (a)
-
By the divergence theorem,
 Vol
Vol
where is
is  with the opposite normal and
with the opposite normal and 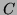 is the solid
cone. Therefore,
is the solid
cone. Therefore,

- (b)
-
Volume of solid is
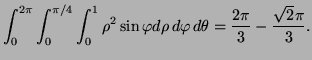
So the volume of the cap is By the
divergence theorem
By the
divergence theorem
 Vol of cap
Vol of cap
so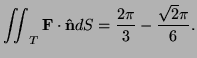
Solution: By the divergence theorem
![]() If
If
![]() then
then
![]() and the volume integral is
and the volume integral is
![]() Vol
Vol![]() Thus the flux of
Thus the flux of ![]() through
through ![]() cannot be
zero, so
cannot be
zero, so
![]() at some point on
at some point on ![]() and therefore
and therefore
![]() cannot be tangent to the surface everywhere.
cannot be tangent to the surface everywhere.
Solution: If
![]() then
then
![]() precisely the given condition
that
precisely the given condition
that ![]() satisfy Laplace's equation. The by the divergence theorem the flux
of
satisfy Laplace's equation. The by the divergence theorem the flux
of ![]() through any closed surface is
through any closed surface is
![]()