


Next: About this document ...
18.02 Practice Exam 2 -- March, 1997 partial solutions soon
Problem 1 (30 points) All six parts refer to the
function
- 1.
- Draw five reasonably spaced level curves for
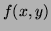 in
the
in
the 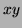 -plane; label each with the corresponding value of
-plane; label each with the corresponding value of 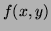 .
.
- 2.
- Let
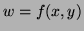 . Find
. Find
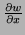 and
and
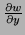 .
.
- 3.
- Find the gradient vector
 at any point
at any point 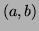 where it is defined, and show by
calculation that it is perpendicular to the level curve of
where it is defined, and show by
calculation that it is perpendicular to the level curve of
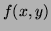 passing through
passing through 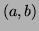 .
.
- 4.
- Find the directional derivative
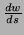 at the
point
at the
point 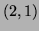 in the direction of the vector
in the direction of the vector
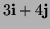 .
.
If you start at this point and go in this direction,
approximately what distance would you travel to decrease the value
of 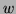 by
by 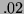 ?
?
- 5.
- Find the point
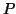 on the graph of
on the graph of 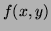 lying over the
point
lying over the
point 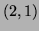 in the
in the 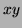 -plane, and find the tangent plane to
the graph at the point
-plane, and find the tangent plane to
the graph at the point 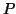 .
.
- 6.
- Give an approximate expression for
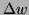 in terms of
in terms of
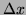 and
and  , for values of
, for values of 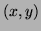 close to
close to
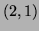 . Use it to answer the two questions below.
. Use it to answer the two questions below.
Near 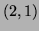 , is the value of
, is the value of 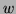 more sensitive to
more sensitive to 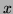 or to
or to
 ?
?
Near 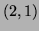 , if an error of
, if an error of 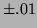 is made measuring
is made measuring 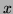 and
and
 , what is the possible resulting error in the corresponding
value of
, what is the possible resulting error in the corresponding
value of 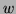 ?
?
Partial solution:
b)
The level curve through 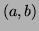 is
is 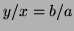 that is
that is 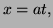
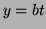 which is a
straightline with tangent vector
which is a
straightline with tangent vector
 d)
The directional derivative is
d)
The directional derivative is
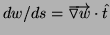 where
where  is a unit vector in give
direction. Thus the directional derivative is
Since
is a unit vector in give
direction. Thus the directional derivative is
Since
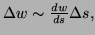 should go approximately
should go approximately 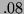 backwards.
backwards.
e) Point on graph is
 Tangent plane to
Tangent plane to 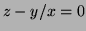 is
is
f)
is more sensitive to changes in 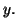 Possible error is
Possible error is
Problem 2 (30 points) A box is to be constructed from
wood pieces of uniform thickness so that the top and two opposite
sides use a single thickness of wood, while the two ends and the
bottom use a double thickness. The volume is to be 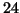 cubic
feet.
cubic
feet.
What dimensions for the box will use the least amount of wood?
- 1.
- Using
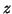 for the height and
for the height and 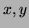 for the other two
dimensions, show the function to be minimized has the form
(
for the other two
dimensions, show the function to be minimized has the form
(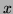 and
and  could be interchanged):
could be interchanged):
- 2.
- Find the
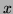 ,
,  and
and 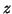 values which minimize
values which minimize 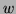 .
.
- 3.
- If the problem is solved using Lagrange multipliers, what
is the value of the multiplier
 corresponding to the
minimum? (To solve this, you do not need to write down all the
equations required by the method.)
corresponding to the
minimum? (To solve this, you do not need to write down all the
equations required by the method.)
Partial solution:
a) The amount of wood is
from top + bottom + sides + ends and given that 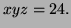
b)
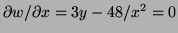 and
and
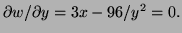 Solving gives
Solving gives 
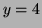 and
and 
c) One Lagrange equation is
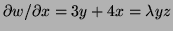 so
so

Problem 3 (10 points) Suppose a change from
 -coordinates to
-coordinates to 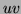 -coordinates is given by the equations
-coordinates is given by the equations
Let 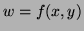 . Then after the change of coordinates,
. Then after the change of coordinates, 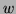 becomes a function of
becomes a function of 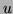 and
and 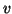 which we shall denote by
which we shall denote by
 , that is,
, that is,
- 1.
- Using the chain rule, express
 and
and
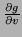 in terms of
in terms of
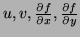 .
.
- 2.
- If
 at the point
at the point
 in the
in the 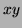 -plane, what is
-plane, what is
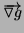 at the point
at the point 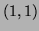 in the
in the 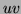 -plane?
-plane?
Problem 4 (10 points) Where does the tangent plane to
the surface
 at the point
at the point 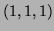 intersect the
intersect the 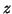 -axis?
-axis?
Partial solution:
Tangent plane is
 intersects the z-axis at
intersects the z-axis at 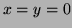 that is
that is 
Problem 5 (10 points) Suppose
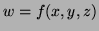 , where
, where
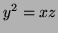 . Express
. Express
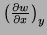 in terms of the partial derivatives
in terms of the partial derivatives 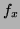 ,
, 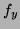 , and
, and
 .
.
Partial solution:
Since 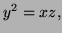
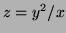 so
so

Problem 6 (10 points) Let  denote the height
of the point
denote the height
of the point 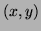 above sea level. A hiker is ascending a
hill. The motion of the hiker is (as observed in the
above sea level. A hiker is ascending a
hill. The motion of the hiker is (as observed in the
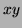 -plane, i.e., on a topographic map of the hill) has these two
properties:
-plane, i.e., on a topographic map of the hill) has these two
properties:
- 1.
- It is always in the direction of
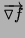 , i.e., perpendicular to the
level curves of
, i.e., perpendicular to the
level curves of 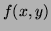 ;
;
- 2.
- Its speed (in the
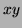 -plane is inversely proportional to
-plane is inversely proportional to
 .
.
Show that the hiker is ascending at a constant rate.
(Express the velocity vector in terms of 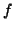 , then use the chain
rule to calculate
, then use the chain
rule to calculate 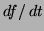 .)
.)



Next: About this document ...
Richard B. Melrose
1999-03-10
![]() by
by ![]() ?
?
![]() , is the value of
, is the value of ![]() more sensitive to
more sensitive to ![]() or to
or to
![]() ?
?
![]() , if an error of
, if an error of ![]() is made measuring
is made measuring ![]() and
and
![]() , what is the possible resulting error in the corresponding
value of
, what is the possible resulting error in the corresponding
value of ![]() ?
?
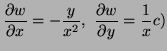

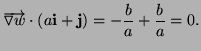
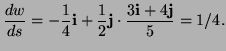
![]() Tangent plane to
Tangent plane to ![]() is
is
![]() cubic
feet.
cubic
feet.
![]() and
and
![]() Solving gives
Solving gives ![]()
![]() and
and ![]()
![]() so
so
![]()
![]() -coordinates to
-coordinates to ![]() -coordinates is given by the equations
-coordinates is given by the equations
![]() at the point
at the point ![]() intersect the
intersect the ![]() -axis?
-axis?
![]() intersects the z-axis at
intersects the z-axis at ![]() that is
that is ![]()
![]() , where
, where
![]() . Express
. Express
![]() in terms of the partial derivatives
in terms of the partial derivatives ![]() ,
, ![]() , and
, and
![]() .
.
![]()
![]() so
so
![]()
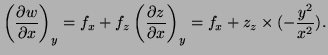
![]() denote the height
of the point
denote the height
of the point ![]() above sea level. A hiker is ascending a
hill. The motion of the hiker is (as observed in the
above sea level. A hiker is ascending a
hill. The motion of the hiker is (as observed in the
![]() -plane, i.e., on a topographic map of the hill) has these two
properties:
-plane, i.e., on a topographic map of the hill) has these two
properties:
![]() , then use the chain
rule to calculate
, then use the chain
rule to calculate ![]() .)
.)