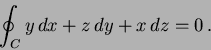Next: About this document ...
18.02 Practice Exam 4 -- May , 1999 2:05-2:55
Directions: Suggested time: 3 hours.
No calculators or notes. There are 20 questions; each counts 12.5 points.
- 1.
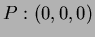
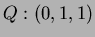
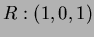 are three points in space. Find the angle between the vectors
are three points in space. Find the angle between the vectors
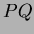 and
and 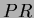 .
.
- 2.
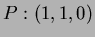
 and
and 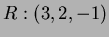 are three points.
are three points.
- (a)
- Find the cross product
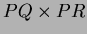 .
.
- (b)
- Using (a), get the equation of the plane through the three
points, in the form
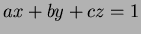 .
.
- 3.
- For what value(s) of the constant
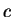 will
the system of equations
will
the system of equations 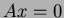 have a non-zero solution, if
have a non-zero solution, if 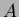 is the matrix shown and
is the matrix shown and 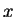 is the column vector?
is the column vector?
- 4.
- Express in terms of
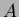 and
and 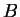 the two
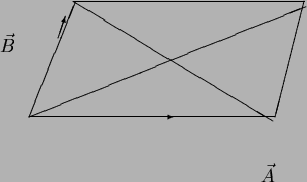
diagonals of the parallelogram shown, and then prove using
vector algebra that if the two diagonals are perpendicular, the
sides of the parallelogram are equal.
the two
diagonals of the parallelogram shown, and then prove using
vector algebra that if the two diagonals are perpendicular, the
sides of the parallelogram are equal.
#1#2#3#4#5@font#3#4#5
- 5.
- The position vector of a moving point
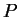 is
is
 .
.
- (a)
- At what point
 does
does  pass through the surface
pass through the surface
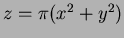 ?
?
- (b)
- What is its speed at that time?
- 6.
- For the function
 ,
and the
point
,
and the
point 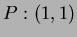 ,
find
,
find
- (a)
- the value of grad
 at
at 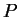 ;
;
- (b)
- the directional derivative
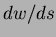 at
at 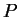 in the direction
of
in the direction
of 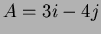 ;
;
- (c)
- starting at
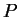 ,
approximately how far should you go in
the direction of
,
approximately how far should you go in
the direction of 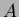 in order to increase the value of
in order to increase the value of  by
by
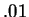 ?
?
- 7.
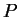 ,
,
 and
and 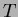 for an ideal gas are related
by
for an ideal gas are related
by  ,
where
,
where 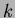 is a constant.
is a constant.
- (a)
- Take
 ,
and give an approximate formula telling how
,
and give an approximate formula telling how
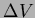 varies with
varies with 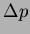 and
and  when
when  and
and  .
.
- (b)
- Continuing part (a), when
 and
and  ,
is
,
is  numerically more sensitive to
numerically more sensitive to 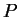 or
or 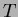 ? (Indicate brief reason.)
? (Indicate brief reason.)
- 8.
- By using Lagrange multipliers, find the point
on the plane
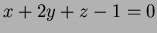 which is closest to the origin.
(Minimize the square of the distance from the origin. If you
don't use Lagrange multipliers, do it some other way for 6 points
credit; L.M.s are the easiest way.)
which is closest to the origin.
(Minimize the square of the distance from the origin. If you
don't use Lagrange multipliers, do it some other way for 6 points
credit; L.M.s are the easiest way.)
- 9.
- Let
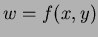 and
and 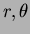 be the usual
polar coordinates. By using the chain rule, find the
be the usual
polar coordinates. By using the chain rule, find the  matrix
matrix  (such that the entries of
(such that the entries of  are explicitly given
functions)
are explicitly given
functions)
- 10.
- For the surface
 ,
find the
tangent plane at
,
find the
tangent plane at 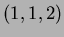 ,
in the form
,
in the form
- 11.
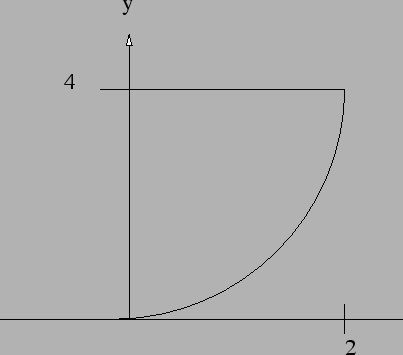
- Evaluate by changing the order of
integration:
- 12.
- Set up an iterated integral in polar
coordinates for the moment of inertia about the origin of the
triangular plate shown. Take the density
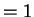 .
Do not evaluate
the integral.
.
Do not evaluate
the integral.
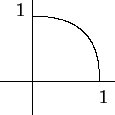
- 13.
- Let
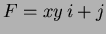 .
Find the work done by
.
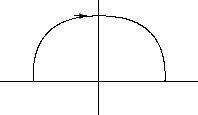
Find the work done by
 going over the quarter-circular path shown, going from
going over the quarter-circular path shown, going from
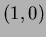 to
to 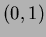 .
.
- 14.
- (a)
- Express the field
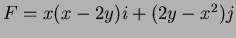 in the form
in the form
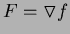 ,
for some function
,
for some function 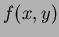 .
Use a systematic method; show work.
.
Use a systematic method; show work.
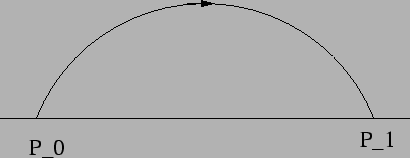
- (b)
- Use this to evaluate
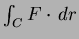 over the
portion of the ellipse given by the graph of
over the
portion of the ellipse given by the graph of 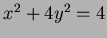 and
lying in the upper half-plane; integrate in the direction left
to right.
and
lying in the upper half-plane; integrate in the direction left
to right.
- 15.
- How should the constants
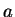 and
and 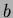 be
related if for any simple closed curve
be
related if for any simple closed curve 
(Give the most general relation; indicate reasoning.)
- 16.
- The solid shown has as its sides the
vertical right circular cone, with vertex at the origin and
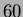 -degree vertex angle. Its top is a portion of the sphere of
the radius
-degree vertex angle. Its top is a portion of the sphere of
the radius 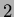 ,
and its bottom is horizontal and flat,
intersecting the cone at a point having distance
,
and its bottom is horizontal and flat,
intersecting the cone at a point having distance  from the
origin. (Cross-section is picture.)
from the
origin. (Cross-section is picture.)
Set up (but do not evaluate) an iterated triple integral in
spherical coordinates giving the gravitational attraction of the
solid on a unit mass placed at the origin. (Take the density
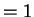 ,
and the gravitational constant
,
and the gravitational constant  .)
.)

- 17.
- Let
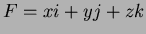 ,
and
,
and 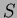 be the closed
cylindrical surface pictured; its sides are the cylinder
be the closed
cylindrical surface pictured; its sides are the cylinder
 ;
its top and bottom are horizontal, at heights
;
its top and bottom are horizontal, at heights 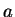 and
and 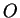 ,
respectively.
,
respectively.
- (a)
- Find the flux of
 over the top and bottom discs.
over the top and bottom discs.
- (b)
- Using part (a) and the divergence theorem, find the flux of
 across the side cylinder.
across the side cylinder.
#1#2#3#4#5#3#4#5

- 18.
- Referring to problem 17, find the flux of
 across the side cylinder by evaluating a surface integral
directly (i.e., without using the divergence theorem).
across the side cylinder by evaluating a surface integral
directly (i.e., without using the divergence theorem).
- 19.
- For what value(s) of the constants
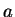 and
and
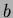 will the line integral
will the line integral
be independent of the path? (Show work.)
- 20.
- By using Stokes' theorem, prove that
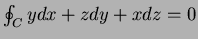 around any simple closed curve lying in
the plane
around any simple closed curve lying in
the plane 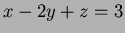 .
.
Brief Solutions:
- 1.
-
so
hence
 angle between
angle between  and
and 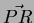 .
Since angle is less that
.
Since angle is less that  ,
angle
,
angle  .
.
- 2.
-
- (a)
-
 .
.
- (b)
- Since this is a normal to the plane, it must be
substituting  so plane is
so plane is
- 3.
- It will have a non-zero solution if and only
if
- 4.
- Diagonals are
 and
and 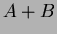 .
These are
perpendicular if
.
These are
perpendicular if
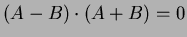 ,
so
,
so
hence
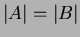 and the side lengths
are equal.
and the side lengths
are equal.
- 5.
-
- (a)
- Passes through
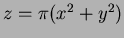 if
if
- (b)
-
so speed  .
.
- 6.

- (a)
-
 at
at  .
.
- (b)
-
- (c)
- Approximately
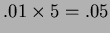 .
.
- 7.
- (a)
-
- (b)
- More sensitive to
 .
.
- 8.
- Lagrange multiplier
Closest point is
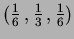 .
.
NB It is easier to look at the normal
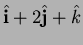 and see where the line in this direction meets
the plane
and see where the line in this direction meets
the plane
Point is
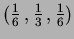 .
.
- 9.
-
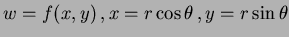
- 10.
-
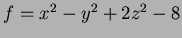 .
Normal to surface is
.
Normal to surface is
Tangent plane is

- 11.
- 12.
- Twice integral for upper half:
- 13.
-
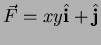 .
Parameterization
.
Parameterization
- 14.
- (a)
-
Thus  is the gradient
is the gradient
 .
.
- (b)
-
- 15.
- By Green's theorem
For this to be 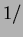 the area, must have
the area, must have 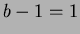 always.
always.
- 16.
- Question is confusing without picture. I
think it should be:
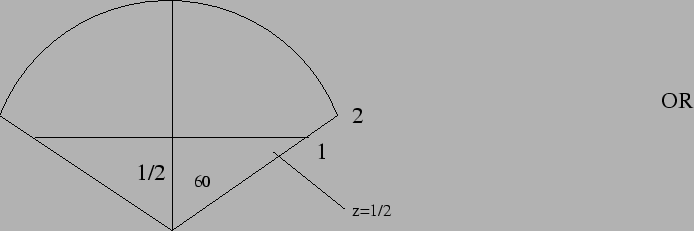
In spherical coordinate 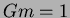 )
)
Bottom plane in
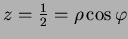 .
.
- 17.
- (a)
-
- (b)
-
where 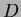 is the interior of the cylinder. Thus the flux through
the sides is
is the interior of the cylinder. Thus the flux through
the sides is 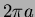 .
.
- 18.
-
For the side surface
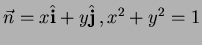 so the flux through the sides in the area,
so the flux through the sides in the area, 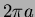 .
.
- 19.
- (Note this has been corrected.) The line
integral is independent of the path only if
is a gradient.
- 20.
- By Stokes' theorem
Since
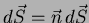 ,
,

for any surface contained in 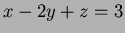 .
Thus
.
Thus



Next: About this document ...
Richard B. Melrose
1999-05-10
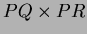 .
.
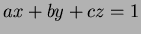 .
.
![\begin{eqnarray*}
A= \left[
\begin{array}{ccc}
1 &0 &c\\
2 &1 &-1\\
1 &2 ...
...[
\begin{array}{c}
x \\
y \\
z
\end{array} \right] \, .
\end{eqnarray*}](img15.png)

 does
does 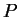 pass through the surface
pass through the surface
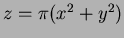 ?
?
 at
at 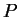 ;
;
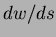 at
at 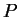 in the direction
of
in the direction
of 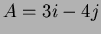 ;
;
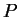 ,
approximately how far should you go in
the direction of
,
approximately how far should you go in
the direction of 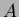 in order to increase the value of
in order to increase the value of  by
by
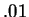 ?
?
 ,
and give an approximate formula telling how
,
and give an approximate formula telling how
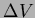 varies with
varies with 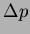 and
and  when
when  and
and  .
.
 and
and  ,
is
,
is  numerically more sensitive to
numerically more sensitive to 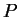 or
or 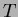 ? (Indicate brief reason.)
? (Indicate brief reason.)
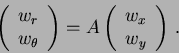



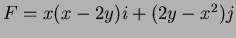 in the form
in the form
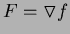 ,
for some function
,
for some function 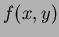 .
Use a systematic method; show work.
.
Use a systematic method; show work.
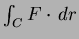 over the
portion of the ellipse given by the graph of
over the
portion of the ellipse given by the graph of 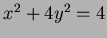 and
lying in the upper half-plane; integrate in the direction left
to right.
and
lying in the upper half-plane; integrate in the direction left
to right.

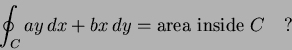
![]() ,
and the gravitational constant
,
and the gravitational constant ![]() .)
.)

 over the top and bottom discs.
over the top and bottom discs.
 across the side cylinder.
across the side cylinder.

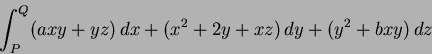
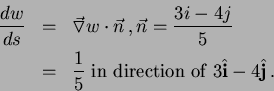
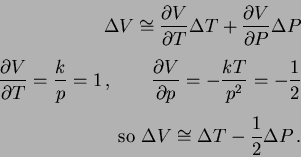
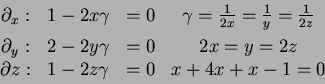
![\begin{eqnarray*}
\begin{array}{lll}
w_r = & \frac{\partial f}{\partial x} \fra...
...heta} \qquad &
w_y= \partial f / \partial y \\ [1ex]
\end{array}\end{eqnarray*}](img111.png)



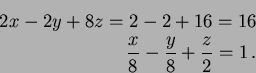

![\begin{eqnarray*}
\int^2_0 \int^4_{x^2} x e^{-y^2} \, dy \, dx \\
&=& \int^4_0...
...^2} \right]^4_0 \\
&=& \frac{1}{4} \left( 1-e^{-16} \right)\, .
\end{eqnarray*}](img119.png)
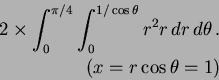

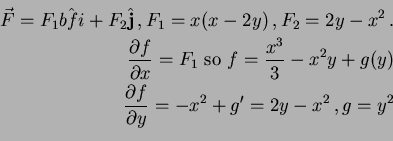

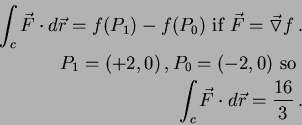
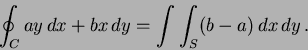


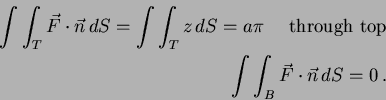
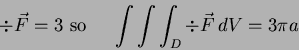
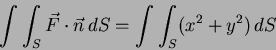
![\begin{eqnarray*}
\frac{\partial F_1}{\partial y} &=& ax+z \, , \frac{\partial
...
...bx \Rightarrow b=1 \\ [1ex]
\hbox{So only if } a=2 \, , b=1 \, .
\end{eqnarray*}](img142.png)