Using the Divergence Theorem, evaluate the flux integral
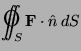 |
where
Solution: By the divergence theorem this flux integral is equal to the volume integral
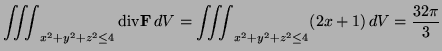 |
by symmetry and the formula for the volume of a sphere.
Solution: The surface area is given by the integral
![]() We
may use the variables
We
may use the variables ![]() and
and ![]() on the surface, the `shadow region' is
on the surface, the `shadow region' is
![]() and the surface measure is
and the surface measure is
Thus the surface area is
![\begin{multline*}
\iint_{\{x^2+y^2\le1\}}(1+4x^2+4y^2)^{\frac12}\,dx\,dy
=\int_0...
...\frac1{12}(1+4r^2)^{\frac32}\big]_0^1=\frac16\pi(5^{\frac32}-1).
\end{multline*}](img14.png)
- (a)
- Sketch the region
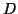 .
.
- (b)
- Using cylindrical (polar) coordinates compute the moment
of inertia of
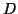 , assumed to have unit density, around the
, assumed to have unit density, around the 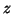 -axis.
-axis.
Solution: a) Anything reasonable! It lies over
![]() with
with
![]()
b)
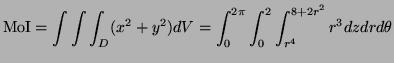 |
|||
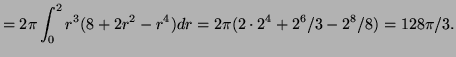 |
Let ![]() be the region in three dimensional space consisting of
the points
be the region in three dimensional space consisting of
the points ![]() with
with ![]() ,
, ![]() ,
, ![]() and
and
![]() .
.
Assuming where needed that ![]() has unit density, write down
integral formulae in terms of spherical coordinates (DO NOT
EVALUATE) for
has unit density, write down
integral formulae in terms of spherical coordinates (DO NOT
EVALUATE) for
- (a)
- The average over
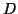 of the distance from the
of the distance from the 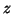 -axis.
-axis.
- (b)
- The moment of inertia of
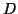 , with unit density,
around the
, with unit density,
around the 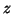 -axis.
-axis.
- (c)
- The
 component of the gravitational force
exerted by
component of the gravitational force
exerted by 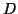 on a unit
mass at the origin.
on a unit
mass at the origin.
Solution: The region in spherical coordinates is
![]()
![]() and
and
![]() Thus the three integrals are
Thus the three integrals are
- (a)
-
 (or an integral for the volume can be written out).
(or an integral for the volume can be written out).
- (b)
-
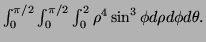
- (c)
-
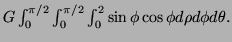
Let ![]() be `ice-cream cone' consisting of the points in the unit ball
(=solid unit sphere) where the `azimuth' (angle with the positive direction
of the z-axis)
be `ice-cream cone' consisting of the points in the unit ball
(=solid unit sphere) where the `azimuth' (angle with the positive direction
of the z-axis)
![]() Assuming that it has unit density, compute the
gravitational force
Assuming that it has unit density, compute the
gravitational force ![]() exerts on a unit mass at the origin.
exerts on a unit mass at the origin.
Solution: Place ![]() so that its axis is the z-axis (as
indicated). Then in spherical polar coordinates the
so that its axis is the z-axis (as
indicated). Then in spherical polar coordinates the ![]() component
(and hence the actual) gravitational force on a unit mass at the origin is
component
(and hence the actual) gravitational force on a unit mass at the origin is
![$\displaystyle G\int_0^{2\pi}\int_0^{\pi/4}\int_0^1 \frac{\cos\varphi }{\rho ^2}...
...phi d\rho\, d\varphi \,d\theta =2\pi G[\frac12\sin^2\varphi]_0^{\pi/4}=\pi G/2.$](img39.png) |