Solution: The moment of inertia around the z-axis is the integral
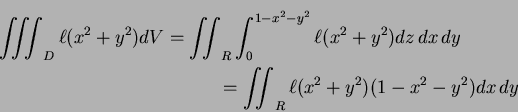
MoI![$\displaystyle =\int_0^{2\pi}\ell\int_0^1(1-r^2)r^2\,rdr\,d\theta =2\pi\ell\big[\frac14r^4-\frac16r^6\big]_0^1=\frac\pi6\ell.$](img9.png) |
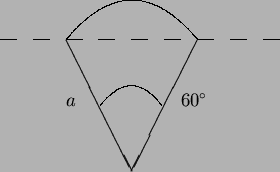
The cone has slant height ![]() and a vertex angle
and a vertex angle ![]() degrees as
pictured.
degrees as
pictured.
Take the density to be ![]() , and find the gravitational attraction
of
, and find the gravitational attraction
of ![]() on a unit mass placed at the vertex. (Set up and evaluate
a triple integral in spherical coordinates.)
on a unit mass placed at the vertex. (Set up and evaluate
a triple integral in spherical coordinates.)
Solution: By symmetry, the gravitational attraction on a unit mass
at the origin is in the direction of the z-axis and hence equal to its
![]() component. This is
component. This is
![\begin{multline*}
G\iiint_D \frac{\cos\varphi}{\rho ^2}dV =\int_0^{2\pi}\int_0^{...
...\theta\\
=G2\pi a\big[\frac12\sin^2\varphi ]^{\pi/6}_0=Ga\pi/4.
\end{multline*}](img15.png)
Solution: Instead the integral becomes
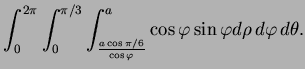 |
Show that ![]() has no net flux through any simple closed curve
has no net flux through any simple closed curve ![]() .
.
This should not really have been on this practice exam. Better do one for flux through a surface.
Solution:
![]() The flux form of Green's
theorem for a simple closed curve
The flux form of Green's
theorem for a simple closed curve ![]() is
is
 |
Since
Let ![]() be the hemisphere of radius
be the hemisphere of radius ![]() , with base in the
, with base in the
![]() -plane and center at the origin, and
-plane and center at the origin, and ![]() be its base (the
disc of radius
be its base (the
disc of radius ![]() and center at the origin in the
and center at the origin in the ![]() -plane).
Both surfaces are oriented so their unit normal vectors point
upwards, i.e., this is the direction of positive flux.
Let
-plane).
Both surfaces are oriented so their unit normal vectors point
upwards, i.e., this is the direction of positive flux.
Let
![]() .
.
- (a)
- Find the flux of
 over
over  , by inspection.
, by inspection.
- (b)
- Using your answer to part (a), find the flux of
 over
over
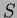 by using the divergence theorem.
by using the divergence theorem.
- (c)
- Find the flux of
 over
over 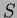 directly, by calculating a
surface integral using spherical coordinates.
directly, by calculating a
surface integral using spherical coordinates.
Solution:
- (a)
- On
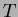 the normal upward normal is
the normal upward normal is 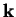 so
so
 and hence the flux upward through
and hence the flux upward through 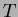 is the area
is the area 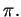
- (b)
- If
 is the upward unit normal to both
is the upward unit normal to both 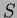 and
and 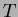 then
by the divergence theorem
then
by the divergence theorem
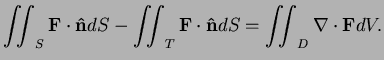
The divergence is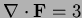 so
so
 Vol
Vol
- (c)
- The flux integral written explicitly is
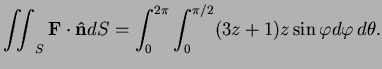
Here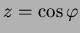 on
on  so this flux integral is
so this flux integral is
![\begin{multline*}
2\pi\int_0^{\pi/2}(3\cos^2\varphi\sin\varphi+\cos\varphi \sin\...
...\big[-\cos^3\varphi -\frac12\cos^2\varphi \big]_0^{\pi/2}
=3\pi.
\end{multline*}](img36.png)