the surface
Solution: The volume is given by the double integral over the region,
![]()
![\begin{multline*}
\iint_R (4-x^2-y^2)dA=\int_0^{2\pi}\int_0^{2}(4-r^2)r\, d\theta\,dr\\
=2\pi\left[2r^2-\frac{r^4}4\right]_0^2=8\pi.
\end{multline*}](img4.png)

Solution: Change the order of integration and the integral becomes
![$\displaystyle \int^1_0 \int^y_0 \cos (y^2) \, dx \, dy= \int_0^1y\cos(y^2)dy=\left[\frac12\sin(y^2)\right]^1_0=\frac12\sin1.$](img6.png) |

Solution: In polar coordinates the integral is
![$\displaystyle \int_0^{2\pi}\int_0^1 \exp (r^2) \, rdr\,d\theta = 2\pi\left[\frac12\exp(r^2)\right]_0^1=\pi(e-1).$](img10.png) |
- (a)
-
For what values of the constant
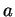 is
a conservative vector field?
is
a conservative vector field?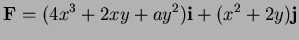
- (b)
-
For
 compute
where
compute
where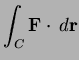
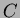 is the semicircule with radius
is the semicircule with radius 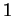 , center
, center 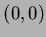 from
from 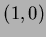 to
to 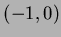 in the upper half-plane.
in the upper half-plane.
Solution:
- (a)
-
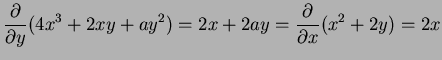
exactly when
- (b)
- Since the vector field is conservative the integral is the same for
any contour with these two endpoints, for instance the segment
![$ [-1,1]$](img21.png) of the
x-axis. The integral along the x-axis is
of the
x-axis. The integral along the x-axis is
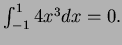
- (a)
- For the vector field
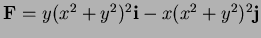 compute
compute
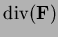
- (b)
- For this vector field and the curve
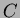 which is the circle of radius
which is the circle of radius
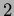 with center the origin and positive orientation, use Green's theorem
to compute the flux integral
with center the origin and positive orientation, use Green's theorem
to compute the flux integral
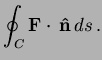
Solution:
- (a)
![\begin{multline*}
\operatorname{div}({\bf F})=\frac{\partial}{\partial x}[y
(x^2...
...al}{\partial y}[x(x^2 +
y^2)^2]\\
=4xy(x^2+y^2)-4xy(x^2+y^2)=0.
\end{multline*}](img27.png)
- (b)
- 0
- (a)
- Why is it closed?
- (b)
- Why is it simple?
- (c)
- Use Green's theorem to express the area inside the curve as a single integral. Do not evaluate it.
OR simply:
Use Green's theorem to express the area inside the simple closed curve
Solution: [There is of course a small conceptual problem here that the curve is not smooth, but I don't suppose that anyone will notice.]
- (a)
-

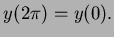
- (b)
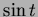 takes each value between
takes each value between 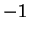 and
and 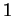 twice for
twice for 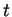 in the
interval
in the
interval ![$ [0,2\pi]$](img35.png) but at these points
but at these points 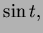 and hence
and hence  has
opposite sign.
has
opposite sign.
- (c)
-


Solution: For ![]() and
and ![]() the Jacobian is
the Jacobian is
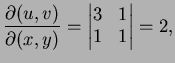
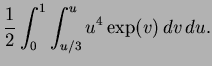 |