Directions: Suggested time: 70 minutes.
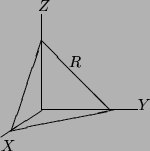
Problem 1 (15 points) The solid ![]() is the piece of
the first octant cut off by the plane
is the piece of
the first octant cut off by the plane
Problem 2 (15 points) A circular disc has radius ![]() and
and ![]() is a point on its circumference. The density at any
point
is a point on its circumference. The density at any
point ![]() on the disc is equal to the distance of
on the disc is equal to the distance of ![]() from
from ![]() .
Set up an iterated double integral in polar coordinates which
gives the mass of the disc. Place
.
Set up an iterated double integral in polar coordinates which
gives the mass of the disc. Place ![]() at the origin. (Give the
integrand and limits, but to not evaluate the integral.)
at the origin. (Give the
integrand and limits, but to not evaluate the integral.)
Problem 3 (15 points) Evaluate the integral
![]() by changing the order of
integration. (Sketch the region of integration first.)
by changing the order of
integration. (Sketch the region of integration first.)
Problem 4 (10 points) Change
![]() to an interated integral in polar
coordinates. (Do not evaluate it.)
to an interated integral in polar
coordinates. (Do not evaluate it.)
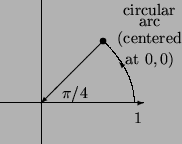
Problem 5 (30 points; 10 each)
Problem 6 (30 points; 15, 5, 10)
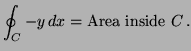
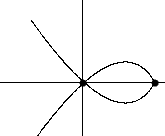
Find the area inside the loop.
Problem 7 (15 points; 5, 10)
![]() is the unit semi-circle in the upper half-plane, running
from
is the unit semi-circle in the upper half-plane, running
from ![]() to
to ![]()
![]() is the line segment from
is the line segment from ![]() to
to ![]()
Brief solutions.
Problem 1

Thus the volume is
![]() OR
OR
![]()
Problem 2
With the center on the x-axis

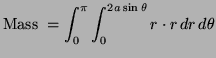
Problem 3
The region of integration for
![]() is
is
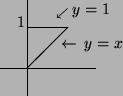
so the integral becomes
![]() ,
which evaluates by
,
which evaluates by
Inner:![$ \left. \cos (y^2) \cdot x\right]^1_0 = \cos (y^2) \cdot y$](img47.png)
Outer:![$ \left. \frac{1}{2} \sin (y^2) \right]^1_0 =\frac{1}{2} \sin 1$](img48.png)
Problem 4
The region of integration for
![]() is
is
![]()

so in polar coordinates the integral becomes
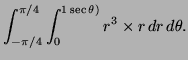
Problem 5
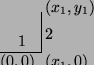
![]() since along
since along ![]()
![]()
![]()
![]()
since
![]() along path
along path ![]()
OR
 |

OR
Since ![]() is path-independent, we can replace
is path-independent, we can replace ![]() by a path
by a path ![]() on the
on the
![]() -axis:
-axis:

Problem 6
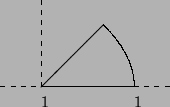
![$\displaystyle = \int^{\pi / 4}_0 \int^1_0 r^2 \cdot r\, dr\,d \theta =
\left. \frac{\pi}{4} \cdot \frac{r^4}{4} \right]^1_0 =
\frac{\pi}{16}.
$](img71.png)
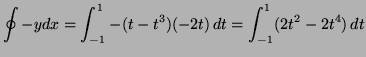 |
|||
![$\displaystyle \left. \frac{2t^3}{3}- \frac{2t^5}{5} \right]^1_{-1} =
\frac{2}{3} - \frac{2}{5} -(\frac{-2}{3} + \frac{2}{5}) = 8/15$](img75.png) |
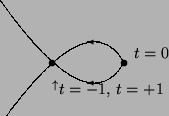
Problem 7
For ![]()
![]() and
and ![]() have the same direction and both are constant
(on
have the same direction and both are constant
(on ![]() , so the work is simply
, so the work is simply
![]() (distance)
(distance)
![]()