


Next: About this document ...
Exam 1 for 18.02, Spring 1999
Your Name:
Recitation Instructor
Recitation Time
For full credit try all problems. Write your name on each page and try if
possible to do all your work on these pages. If it is necessary to add some
more pages, write your name on each.
Marks:
- 1.
- 2.
- 3.
- 4.
- 5.
Problem 1 (20 points; 7, 6, 6) Let
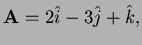
 .
.
- 1.
- For what values of
 will
will  and
and 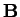 be perpendicular?
be perpendicular?
- 2.
- For what values of
 will
will  and
and  be parallel?
be parallel?
- 3.
- If
 find
find
 where
where  is the angle between
is the angle between  and
and 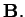
Solution
- 1.
- The dot product is
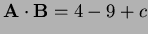 which vanishes exactly
when
which vanishes exactly
when  So
So  and
and 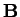 are perpendicular when
are perpendicular when  only.
only.
- 2.
- The cross product is
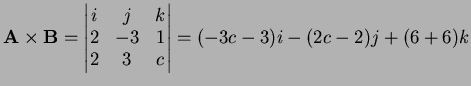 can never vanish, so
can never vanish, so  and
and 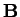 are not perpendicular for any
value of
are not perpendicular for any
value of  (Nasty huh!)
(Nasty huh!)
- 3.
- If
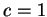 then
then
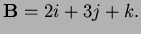 Both
Both  and
and 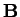 have
length
have
length  and
and
 so
so
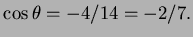
Problem 2 (20 points;7,7,6) Consider the three points
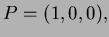
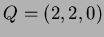 and
and

- 1.
- Find the area of the triangle with these points as vertices.
- 2.
- Give the equation of the plane through these three points in the form
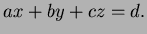
- 3.
- Find parametric equations for the line which passes through the
point
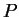 and is perpendicular to the plane through
and is perpendicular to the plane through 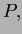
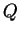 and
and 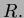
Solution
- 1.
- The area of the triangle is
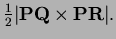 Since
Since
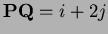 and
and
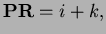
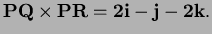 Thus
the area of the triangle is
Thus
the area of the triangle is 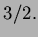
- 2.
- Since the normal to the plane is
 it is given
by the equation
it is given
by the equation
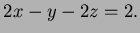
- 3.
- This line has direction
 so has parametric
equations
so has parametric
equations 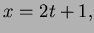
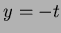 and
and 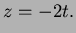 (Other forms are possible.)
(Other forms are possible.)
Problem 3 (25 points; 5, 10, 5, 5) Consider the system of equations
- 1.
- Write these equations in matrix form
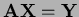 where
where
 is a matrix and
is a matrix and 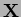 and
and  are column vectors.
are column vectors.
- 2.
- Set
 and find
and find
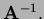
- 3.
- Use your computation of
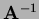 to solve the equations when
to solve the equations when 
- 4.
- For which value(s) of
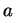 does the homogeneous equation
does the homogeneous equation
 not have a unique solution?
not have a unique solution?
Solution
- 1.
- These equations are of the form
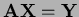 if
if
- 2.
- If
 the determinant is
the determinant is
Then successively the minor, cofactor, transpose cofactor and inverse
matrices are
![\begin{multline*}
\left[\begin{matrix}8&8&6\\ 2&2&0\\ -4&-1&-3\end{matrix}\right...
...trix}-4/3&1/3&2/3\\ 4/3&-1/3&-1/6\\ -1&0&1/2\end{matrix}\right].
\end{multline*}](img53.png)
- 3.
- The solution is
![$ {\bf X}={\bf A}^{-1}{\bf Y}=
\left[\begin{matrix}13/3\\ 1/6\\ 7/2\end{matrix}\right]$](img54.png) so
so 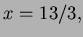
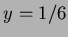 and
and 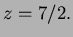
- 4.
- The determinant vanishes only if
 so for this value the
homogeneous equation
so for this value the
homogeneous equation
 does not have a unique solution.
does not have a unique solution.
Problem 4 (20 points; 5, 5, 5, 5) The coordinates of a moving
point satisfy the parametric equations
- 1.
- At what point does it meet the plane
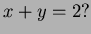
- 2.
- Calculate the velocity at this point.
- 3.
- What is the acceleration at his point?
- 4.
- Find the point where the speed is smallest.
Solution
- 1.
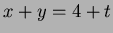 on the curve, so
on the curve, so 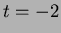 and hence
and hence 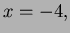


- 2.
- The velocity curve is
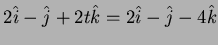 at the point of intersection with the plane.
at the point of intersection with the plane.
- 3.
- The acceleration is constant and is
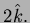
- 4.
- The square of the speed for any
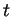 is
is  which takes its
minimum value
which takes its
minimum value 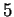 at
at  Thus the point at which the speed is smallest
is
Thus the point at which the speed is smallest
is 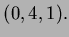
Problem 5 (15 points) Using vector methods show that the
midpoints of the sides of any quadrilateral in the plane are the corners of a
parallelogram.
Solution This is a proof from class. If the vertices in clockwise
order are 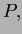
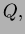
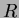 and
and 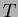 then four sides of the quadrilateral with
vertices the midpoints of the sides of the given quadrilateral are, in order,
then four sides of the quadrilateral with
vertices the midpoints of the sides of the given quadrilateral are, in order,
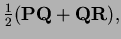
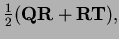
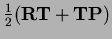 and
and
 Since
Since
 the first and third sides sum to zero and similarly
the second and last sum to zero, so this is a parallelgram.
the first and third sides sum to zero and similarly
the second and last sum to zero, so this is a parallelgram.



Next: About this document ...
Richard B. Melrose
1999-05-11
![]()
![]() .
.
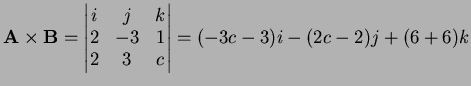 can never vanish, so
can never vanish, so ![]()
![]() and
and
![]()
![$\displaystyle {\bf A}=\left[\begin{matrix}1&1&-1\\ 3&0&-4\\ 2&a&0\end{matrix}...
...d{matrix}\right],\ {\bf Y}=\left[\begin{matrix}1\\ -1\\ 9\end{matrix}\right].$](img51.png)
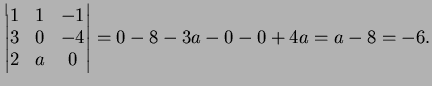
![\begin{multline*}
\left[\begin{matrix}8&8&6\\ 2&2&0\\ -4&-1&-3\end{matrix}\right...
...trix}-4/3&1/3&2/3\\ 4/3&-1/3&-1/6\\ -1&0&1/2\end{matrix}\right].
\end{multline*}](img53.png)
![$ {\bf X}={\bf A}^{-1}{\bf Y}=
\left[\begin{matrix}13/3\\ 1/6\\ 7/2\end{matrix}\right]$](img54.png) so
so ![]()
![]()
![]() and
and ![]() then four sides of the quadrilateral with
vertices the midpoints of the sides of the given quadrilateral are, in order,
then four sides of the quadrilateral with
vertices the midpoints of the sides of the given quadrilateral are, in order,
![]()
![]()
![]() and
and
![]() Since
Since
![]() the first and third sides sum to zero and similarly
the second and last sum to zero, so this is a parallelgram.
the first and third sides sum to zero and similarly
the second and last sum to zero, so this is a parallelgram.