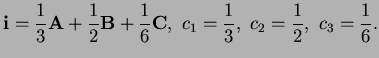Next: About this document ...
Practice Exam 1 for 18.02, Spring 1999
Problem 1 (25 points; 10, 10, 5) Let
 ,
,
 .
.
- 1.
- Find a vector perpendicular to both
 and
and 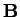 .
.
- 2.
- Find the equation of the plane passing through the
point
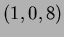 and parallel to both
and parallel to both  and
and 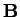 .
.
- 3.
- Determine where the plane meets the
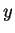 -axis.
-axis.
Solution
- 1.
-
 is perpendicular to both.
is perpendicular to both.
- 2.
- The plane is
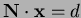 so
so 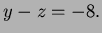
- 3.
- It meets the
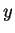 -axis (which is
-axis (which is 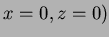 at the point
at the point 
Problem 2 (15 points) Use vector methods to show that
the line joining the mid-points of two sides of a triangle is
parallel to the third side.
Solution If the vertices of the triangle are 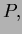
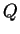 and
and  then
the sides are
then
the sides are 
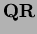 and
and  The vector from the
midpoint of PQ to the midpoint of
The vector from the
midpoint of PQ to the midpoint of  is
is
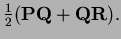 Summing
the three sides gives zero so
Summing
the three sides gives zero so
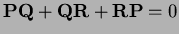 which implies
that
which implies
that
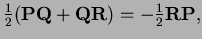 so the line between the
midpoints of two sides is parallel to the base
so the line between the
midpoints of two sides is parallel to the base 
Problem 3 (25 points; 20, 5) Consider the system of
linear equations
- 1.
- Take
 . Write the system in matrix form
. Write the system in matrix form 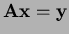 .
Calculate
.
Calculate
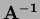 and use it to find equations expressing
and use it to find equations expressing
 ,
,  ,
, 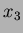 in terms of
in terms of  ,
, 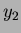 and
and  .
.
- 2.
- For what value(s) of
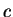 is it not possible to
solve for the
is it not possible to
solve for the 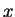 's in terms of the
's in terms of the 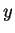 's?
's?
Solution
- 1.
- The matrix
![$ {\bf A}=
\left[\begin{matrix}2&3&c\\ -1&0&1\\ 1&1&1\end{matrix}\right].$](img40.png) For
For  the
cofactor matrix of this is
the
cofactor matrix of this is
![$ \left[\begin{matrix}-1&2&-1\\ 0&-1&1\\ 3&-5&3\end{matrix}\right].$](img41.png) The
determinant (in general) is
The
determinant (in general) is
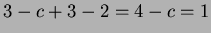 when
when  Thus the inverse
matrix is
Thus the inverse
matrix is
![$ \left[\begin{matrix}-1&0&3\\ 2&-1&-5\\ -1&1&3\end{matrix}\right].$](img44.png) It follows that
It follows that
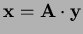 so
so
- 2.
- For
 since the determinant of
since the determinant of  vanishes and there is
then either no solution or an infinite number of solutions depending on
vanishes and there is
then either no solution or an infinite number of solutions depending on
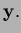
Problem 4 (25 points; 10, 5, 5, 5) The motion of a point
 in space is described by the parametric equations
in space is described by the parametric equations
- 1.
- Does the curve meet the plane
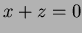 ?
?
- 2.
- Where does the curve meet the plane
 ?
?
- 3.
- Compute the velocity vector for the curve.
- 4.
- Find the point at which the speed is smallest.
Solution
- 1.
- On the curve
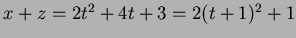 which never vanishes, so the
curve does not meet the plane
which never vanishes, so the
curve does not meet the plane 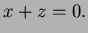
- 2.
- The velocity vector is

- 3.
- The square of the speed is
 so the
minimum occurs at
so the
minimum occurs at 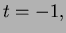 which means at the point
which means at the point 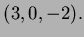
Problem 5 (10 points) Consider the vectors
- 1.
- Show that each is perpendicular to the other two.
- 2.
- Find constants
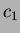 ,
, 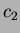 ,
,  so that
so that
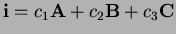 .
.
Solution
- 1.
-
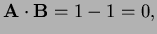

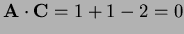 so each is perpendicular to the others.
so each is perpendicular to the others.
- 2.
- The dot products are

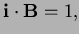
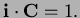 The squares of the lengths are
The squares of the lengths are

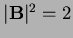 and
and
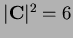 so
so



Next: About this document ...
Richard B. Melrose
1999-02-18
![]() ,
,
![]() .
.
![]()
![]() and
and ![]() then
the sides are
then
the sides are ![]()
![]() and
and ![]() The vector from the
midpoint of PQ to the midpoint of
The vector from the
midpoint of PQ to the midpoint of ![]() is
is
![]() Summing
the three sides gives zero so
Summing
the three sides gives zero so
![]() which implies
that
which implies
that
![]() so the line between the
midpoints of two sides is parallel to the base
so the line between the
midpoints of two sides is parallel to the base ![]()
![$ {\bf A}=
\left[\begin{matrix}2&3&c\\ -1&0&1\\ 1&1&1\end{matrix}\right].$](img40.png) For
For ![$ \left[\begin{matrix}-1&2&-1\\ 0&-1&1\\ 3&-5&3\end{matrix}\right].$](img41.png) The
determinant (in general) is
The
determinant (in general) is
![$ \left[\begin{matrix}-1&0&3\\ 2&-1&-5\\ -1&1&3\end{matrix}\right].$](img44.png) It follows that
It follows that
![]() in space is described by the parametric equations
in space is described by the parametric equations