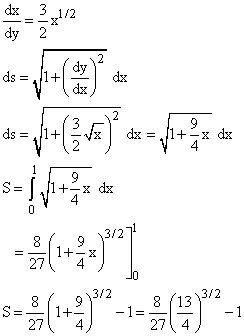|
||
|
|
||
|
To calculate the distance, S, along a curve C between points A and B.
This distance is called arc length of C between A and B.
Let Ds be the distance along the curve between M and N and Dx, Dy their difference in coordinates.
When M and N are very close to each other,

and by the Pythagorean theorem we get
.![]()
We approximate S by a succession of chords, so that the sum of their lengths tends to S as their number increases.
The length S becomes the integral of ds from A to B.
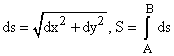
Length S
![]()
If the curve C is expressed by parametric equations x(t), y(t):
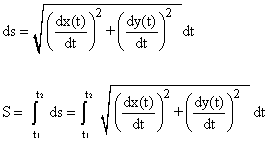
If the curve C is expressed by y = f(x):
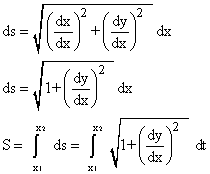
Examples:
Circle
The parametric equations of a circle of radius b are
![]()
Calculate the arc length S of the circle.

Astroid
The parametric equations of an astroid are
x = cos3t
y = sin3t
Calculate the arc length of 1 / 4 of the astroid (0 ![]() t
t ![]()
![]() / 2).
/ 2).
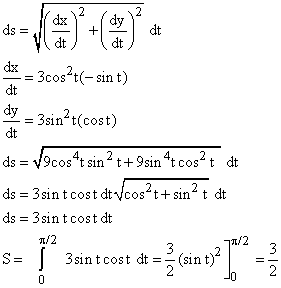
Cycloid
A cycloid is the curve traced out by a point on the circumference of a circle when the circle rolls along a straight line in its own plane. The equations of a cycloid created by a circle of radius 1 are
x(t) = t - sin t
y(t) = 1 - cos t
Calculate the arc length S of the cycloid for 0 ![]() t
t ![]()
![]() / 2.
/ 2.
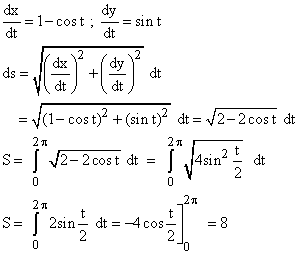
Ball trajectory
The equations of the trajectory of a thrown ball are
x = at
y = bt - 16t2
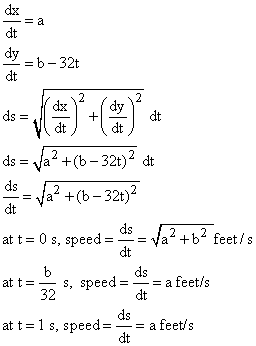
Example 5
Calculate the arc length of y = x2 between x = 0 and x = 2.
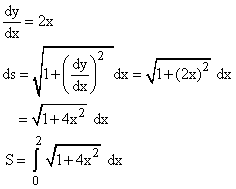
Example 6
Calculate the arc length of the curve y = x3/2 between x = 0 and x = 1.