4. Non-Adaptive Sorting: Batcher's Algorithm
The weighing algorithm we found was non-adaptive. We were able to spell out in advance exactly which side each of the balance each coin would be.
The weighing problem is a special case of the sorting problem where we have the special case that all but one coin or key has the same weight, while in the usual sorting problem, all weights are different.
So we can ask in the sorting problem: can we find a non-adaptive algorithm for it: one for which there are a fixed set of comparisons; the keys are fed in unsorted, and come out after a predetermined set of operations, all sorted.
We will produce just such an algorithm, in which the basic operation is a "compare and switch": given two keys x and y, located in boxes a and b, we compare x and y and put the larger of the two in a and the smaller in b.
We can describe such an operation by setting
New a = max( old a, old b), New b = min( old a, old b).
An algorithm of this kind consists of a sequence of operations every one of which has this form, so it can be described completely by describing which pairs (a,b) are to be treated in this way in each step.
There is a very simple and slick way to do this, called Batcher's algorithm after its discoverer. It is based on the following simple and wonderful fact.
If you have a list of keys arranged from left to right, and you sort the left and right halves of the list separately, and then sort the keys in even positions on the list, and in odd positions separately,
Then all you need do is compare and switch each even key from the left with the odd key immediately to its right, and you will have completely sorted the whole list.
Consider the following example: we start with 8 keys ordered as follows
1 7 3 4 5 2 8 6
Sorting the first and last halves separately changes this to
1 3 4 7 2 5 6 8
Sorting the odd and even placed halves separately and in place changes this to
1 3 2 5 4 7 6 8,
and you will notice that comparison and switching the second and third, fourth and fifth and sixth and seventh finishes the sorting job,
First we will ask, why is this so? Then we will see how to exploit this fact to create a sorting algorithm.
Consider a key in an even position, say the 2kth
after this first, last and odd, even sorts.
If we have 2m keys all together, then we know that there are k-1 even position keys to its left and m-k even position keys to its right.
Each even position key had a unique odd position key to its immediate left that had to be smaller than it after the first round of left right sorts: there are therefore at least k odd position keys that are smaller than the key in position 2k which makes at least 2k-1 smaller keys all together, and so after a complete sort this key belongs at position 2k or to its right.
If we were to do a similar count of keys that
belong to the right of the 2kth key we find that each even position key except
the top key on the left and the top key on the right has an odd key to its
right. Except possibly for these two, the key in 2kth position and every larger
even has an odd key larger than this. So there are m-k-1 odd keys larger than
the key in 2kth position.
There are at least (m-k) even keys that belong to the right of the key at position 2k, and at least (m-k-1) odd keys that belong to its right. This means that in a complete sort this key belongs either at position 2k or 2k+1.
The exact same argument (with left switched for right, etc.) shows that in a complete sort, the odd key in position 2k+1 belonts either at position 2k+1 or 2k.
Thus comparing and switching each even key with
the odd key to its right will finish the sorting job.
What algorithm can we make from this fact?
This fact tells us how to sort 2m keys if we can sort m keys. We can sort left and right sets of m keys, then odd and even, and then do the last round of even odd comparisons and switches.
If we did this the obvious way, to sort n keys we would require 4 sorts of n/2 keys, 16 sorts of n/4 keys, etc. This give us a sorting algorithm which takes around n^2 comparisons, which is really not very efficient at all. How can we do better?
There is a clever way to speed it up. After we sort the left and right halves of the keys, the left and right halves of both the even and the odd keys are already sorted, so we do not have sort lefts and rights in sorting the even and odd keys... We only have to merge the left odd keys with the right odd keys to sort the odd keys, and similarly with the even keys.
Thus if we write the algorithm schematically as
Sort Algorithm for 2m keys = Sort left half and Sort right half; Then Merge the two halves,
we can describe the Merge step as
Merge 2m keys = Merge m odd keys and m even keys. Then compare and switch each even key with odd key to its right.
This is a complete description of the algorithm but it leaves me at least a bit confused as to what it actually does. So let us dig a bit deeper.
A comparison and switch of two keys can be described by an ordered pair of key positions which can be described by a directed edge of a directed graph. The edge will point from the position that is to get the smaller key to the one that gets the larger one.
Suppose for example, we want to sort our initially unsorted keys into pairs. The algorithm for this is not what we have been describing but it is easier. You compare and switch them.
Suppose now we want to sort four keys in positions p1 p2 p3 and p4
We first sort the left and right pairs which can be described by the edges (p1, p2) and (p3, p4).
Then we merge by sorting the odds and evens with edges
(p1, p3) and (p2, p4)
and complete the job with (p2,p3).
We will sort 8 keys this way, and leave the 16 and 32 cases to you.
We
include here a graphic representation of the algorithm. The black lines
represent the keys, and the colored lines represent compare and switch
operations. Time proceeds from left to right.
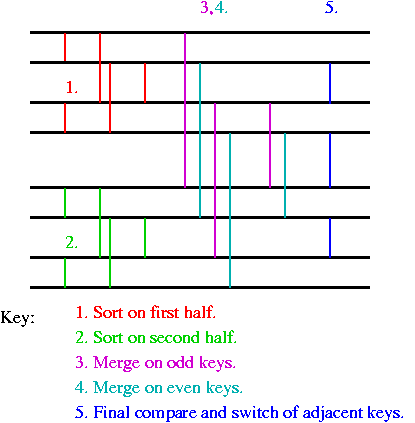
To sort 8 we first apply the sort 4 algorithm to the first half and second half of our keys, separately. This takes the same three rounds of comparison switches just described.
Sort pairs
(p1, p2) (p3, p4) (p5, p6) (p7, p8)
Merge to fours
(p1, p3) ( p2, p4) (p5, p7) (p6, p8)
(p2, p3) (p6, p7)
Now we repeat the merge 4 steps now on odds and evens separately
(p1, p5) (p2, p6) (p3, p7) (p4, p8)
(p3, p5) (p4, p6)
and finally compare and switch evens with next odds:
(p2, p3), (p4, p5), (p6, p7)
Notice that repeating steps on evens and odds, has the effect of doubling the distance between the front and back of each edge and making each edge into two parallel overlapping edges.
How many comparisons does this algorithm take? One way to solve this is to write down the recursion equations. To merge 2^k things [that is, to merge a sorted list of 2^(k-1) with a sorted list of 2^(k-1)], we need to merge 2^(k-1) things twice, and then do 2^(k-1)-1 compare and switch operations. So if we let M(t) be the number of compare and switches we need to merge 2^k things, we get
M(2k) = 2M(2k-1) + 2k-1 – 1.
Now, to sort 2^k things, we need to sort 2^(k-1) things twice, and then do one merge of 2^k things, so if S(2^k) is the number of compare and switches to sort 2^k things, we get
S(2k) = 2S(2k-1) + M(2k).
We can solve these two equations to come up with either an approximate number of comparisons, or if we're more careful, an exact number of comparisons. However, there's an much easier way to figure out roughly how many comparisons it takes. We can count rounds, where a round is a set of comparisons that you can do all at once. Then we can use the fact that each round will involve at most n/2 comparisons. Doing this (which we will leave for a homework assignment) gives us a bound of around 1/4 n (log2 n)2 compare and switches in Batcher's algorithm.
One nice feature of this algorithm which is perhaps not so nice for you, is that it is easy to implement this algorithm on a spreadsheet, where you can put the original keys in the first column, put each round of comparison switches in subsequent columns (using say b1= max(a1,a2), b2=a1-b1+a2 for a comparison and switch). You can then watch your keys get sorted,
This sort is very nice in that there is no
excess movement of keys, no wastage of space, easy to
do in parallel, but unfortunately for huge sorts it takes too many rounds.
For around twenty years after Batcher came up with this algorithm, there was a celebrated open question of whether a sorting network existed that used only O( n log n ) compare and switches. In 1983, Ajtai, Komlos and Szemeredi came up with one, albeit with a horrible constant hidden by the big-O notation. This constant has since been improved to only around 1800 n log2 n compare and switches. This would be better than Batcher's sorting network only when you need to sort something like 2^7200 keys, a number too big to be called astronomical (there aren't that many particles in the universe).