25. Strassen’s Fast Multiplication of Matrices Algorithm, and Spreadsheet Matrix Multiplications
1. Introduction
Suppose we want to multiply two n by n matrices, A and B.
Their product, AB, will be an n by n matrix and will therefore have n2 elements.
Each one of these elements is naturally expressed as the sum of n products, each of an element of A with one of B. Thus we have
(AB)jk = Ss=1s=n AjsBsk,
and the number of multiplications involved in producing the product in this way is n3.
In fact, a matrix product of this kind can be obtained using a smaller number of operations, and we will describe how this can be done.
We will also discuss some curious spreadsheet algorithms for manipulating matrices.
Thus, if we produce the product AB in the usual manner on a spreadsheet with no additional work we can obtain AkB as well, for any k we choose.
Also, with one easy instruction, whose entry is similar to applying the formula for computing the determinant of a 2 by 2 matrix (along with some copying), we can compute the determinant of any square matrix A of any size, and even obtain all the cofactors of the elements A, which is what you need to solve a set of n by n equations.
2. Fast Matrix Multiplication; Partitioning Matrices
We will describe an algorithm (discovered by V.Strassen) and usually called “Strassen’s Algorithm) that allows us to multiply two n by n matrices A and B, with a number of multiplications (and additions) which is a small multiple of n(ln 7)/(ln 2), when n is of the form 2k. This is like 22.8 instead of 23
The algorithm is based upon three ideas.
The first idea is that of “partitioning matrices” which in our context is:
The
multiplication of 4 by 4 matrices A and B is equivalent to the multiplication
of a pair of 2 by 2 matrices whose elements are each 2 by 2 matrices.
In a four by four matrix the indices on row or column range from 1 to 4 In a two by two matrix of two by two matrices there are also four indices on row or column but they are called 11, 12, 21 and 22, the first index here representing the index of one 2 by 2 matrix and the second of the other.
Forming a matrix product is taking a dot product of row components of one with column components of the other. It does not matter in the slightest how you name the components; with either kind of index you multiply each row component of the first by the corresponding column component of the second. In one case this looks like
aj1 * b1k + aj2 * b2k + aj3 * b3k + aj4 * b4k.
while with the other names it looks like
ajk,11 * b11,st + ajk.12 *b12,st + ajk,21 * b21,st + ajk,22 * b22,st .
but who cares? The net result is the same. And as a matter of fact, given n by n matrices A and B for which n is factorable into r and s (n=r*s) you can similarly write them as r by r matrices whose components are each s by s matrices in the same general way without changing the definition of their matrix multiplication at all.
Explicitly, in the 4 by 4 case, if we describe A and B as
 , and
, and 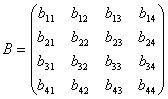
Then their matrix product is exactly the same as the product of the matrices
 and
and
 ,
,
where we have
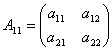 ,
, 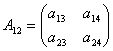 ,
, 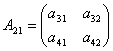 , and
, and 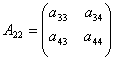 .
.
and
the same kind of thing for B.
Now suppose we have matrices matrices whose dimensions are 2k by 2k. We can represent the indices either as integers from 1 to 2k or as k-tuples, each element of which is 1 or 2. (this is very much like using a binary representation of our indices except that we use 1 instead of 0 and 2 instead of 1 and the all 1’s index here corresponds to 1 while the all 0’s in binary corresponds to 0)
And with
the latter representation we can interpret matrix multiplication as the 2
by 2 product of 2k-1 by 2k-1 matrices each one of which
is a 2 by 2 product of 2k-2 by 2k-2 matrices, and so
on.
The consequence we draw from this fact is: if we can multiply 2 by 2 matrices using only 7 multiplications instead of the usual 8, we can parlay that into multiplying 4 by 4 matrices using 7 multiplications of 2 by 2 matrices each of which requires 7 multiplications of numbers, for a total of 49 multiplications.
Furthermore,
by iterating this fact, we can multiply 2k by 2k
matrices with 7k multiplications of numbers, so long as we can
handle 2 by 2 matrices with 7 multiplications in a way that does not use commutativity.
3. Representing a Matrix Product as a Single Polynomial
From now on then we will consider the problem of computing the 4 entries in the product of two 2 by 2 matrices.
Explicitly, given 2 by 2 matrices with elements aij and bjk we want to compute the four combinations
a11b11 + a12b21, a11b12 + a12b22, a21b11 + a22b21, and a21b12 + a22b22.
The second idea here is that we will get a better grasp of the problem if we combine these four combinations into one entity. And we can do this by multiplying each one by an indeterminate (or variable) and adding them up.
The result will be a polynomial, and our task will be both to compute this polynomial from the a’s and b’s using 7 multiplications, and to find the coefficients of our marker variables in the polynomial.
And here is where we run into amazing luck. If we call our “variables” (or if you prefer “indeterminates”) zkj and multiply the combinations above by z11, z21, z12 and z22 respectively, our polynomial when written out is
a11b11z11 + a12b21z11 + a11b12z21 + a12b22z21 + a21b11z12 + a22b21z12 + a21b12z22 + a22b22z22
which is
Sj,s,k=12 ajsbskzkj.
Our luck is the fact that this polynomial has quite a bit of symmetry.
In particular, we can interchange the subscripts 1 and 2 everywhere, and this combination does not change. Which is to say that for each term (for example the first term) there is another which is its image under changing all the indices (here the last term).
Second, we can permute the indices j s and k, replacing j by s, s by k and k by j, without changing this polynomial, and we can reverse this permutation.
If we perform the first of these two permutations the first and last terms stay fixed, but the term a12b21z11 becomes a21b11z12 (j=1 s=2 k=1 becomes j=2 s=1 k=1) and so on.
Thus there is a group of index changes that leave our polynomial unchanged, and this group has the following six elements:
The identity; permute (j,s,k); permute (j,k,s); switch 1 and 2; switch 1 and 2 and permute (j,s,k); switch 1 and 2 and permute(j,k,s).
The 8 terms in our polynomial form two orbits under the action of this group.
One is the pair consisting of the first and last term above whose indices are all the same. These are stabilized by the identity and by the permutations (j,s,k) and (j,k,s).
The other orbit consists of the remaining terms. Notice that each of these terms has one factor with repeated indices and two factors whose indices are each 12 or 21.
(By the way, you should read (j,s,k) as meaning : the new value of j is the old value of s, the new value of s is the old value of k, and the new k value is the old j value.)
The next question is: how can we exploit this symmetry to find a way to write our polynomial as the sum of 7 products.
4. The Last Idea
First we must introduce a product that will give us the first and last entries.
We can find a single product which has all the same symmetries as our polynomial, that will give us both of these: namely
(a11 +a22) (b11 +b22) (z11 +z22).
If we write this product out, however, it consists of 8 terms, 2 of which are what we want, namely our first and last terms, but there are 6 terms we do not want and of course 6 terms in our polynomial that are not present in this product.
In fact the difference between our matrix-product polynomial and the product
(a11 +a22) (b11 +b22) (z11 +z22).
is given by this twelve term polynomial:
a12b21z11 + a11b12z21 + a12b22z21 + a21b11z12 + a22b21z12 + a21b12z22 - a11b11z22 - a11b22z11 - a11b22z22 - a22b11z11 - a22b11z22 - a22b22z11.
This difference polynomial, being the difference of two polynomials each of which is invariant under the action of our group, is also invariant under this group’s action.
f you look at this difference, it consists of two complete orbits under our symmetry group: in one orbit one factor has two indices the others have both indices in opposite order; in the other all indices are the same in each factor one appearing in two factors and the other in one factor.
We want to find an invariant that will add the positive terms here and get rid of the negative ones and be a sum of six products.
How can we get an invariant here?
There is always an obvious way to find an invariant in situations like this; take one asymmetric term, and look at the sum of the terms in its orbit. This orbit sum will always be invariant!
Thus here we want to find any old single product pair of terms that contains one of each of our positive terms and one of our negative terms. We can apply each of the symmetries in our group to it, and sum the results.
Each term in our product, when summed, will produce an invariant, consisting of six terms. And because the difference polynomial we are looking for consists of the difference of two orbit sums, if we can find a single product that handles one from each orbit of our bad terms, by symmetry, their orbit sums will have them all. So if we can find a single product that cures two bad terms one of each sign it will do what we need here as long as it doesn’t add other garbage.
Suppose we want a term that will produce a12b21z11 - a22b22z11. We can try
(a12 - a22) (b21
+ b22) z11.
.This will do the right thing by giving us two terms we want here:(a12 b21 z11 and –a22 b22 z11 but multiplying it out produces four terms:, it produces two weird extra terms, namely
a12 b22z11 and -a22b21 z11.
And here is the great thing. These two terms are in the same orbit under our group action and have the opposite sign. Both terms have two diagonal factors with opposite coordinate values, and one off diagonal entry, and the signs are opposite. Under the group action each term here will have an orbit consisting of all possible terms with one 11 index pair, one 22 pair and a 12 or 21 pair, In other words, the sum of each of these terms over the orbit will be exactly the same, and so the sum of both will cancel to 0.
And the terms we want will give us the difference in orbits that we want.
Which means we have the answer!
Explicitly, the six products that we want which, when added to
(a11 +a22) (b11 +b22) (z11 +z22) give us our polynomial, are
(a12 - a22) (b21 + b22) z11
(a21 – a11) (b12 + b11) z22
a11 (b12 - b22) (z21 + z22)
a22 (b21 - b11) (z12 + z11)
(a21 + a22) b11 (z12 - z22)
(a12 + a11) b22 (z21 – z11).
And indeed, the sum of the seven products indicated here give us our polynomial.
Let us recall what this means. The products indicated are the products of the a’s and b’s here. The z’s tell us where the products go in the product matrix.
Thus the first term, (a11
+a22) (b11 +b22) (z11 +z22)
says we put the product, (a11 +a22) (b11
+b22) in both the 11 and 22 entries of the product matrix. Similarly,
the second product, (a12 - a22) (b21 + b22)
goes in the 11 entry, and so on; and the last term for example, tells us that
(a12 + a11 ) b22
appears with a positive sign in the 12 entry and with a negative sign in the
11 entry of the matrix. REMEMBER THAT z21 MEANS THAT THE ACCOMPANYING
PRODUCT GOES INTO THE 12 POSITION, NOT THE 21 POSITION!
To take the products indicated of 2j by 2j matrices requires first forming the combinations of a’s and b’s necessary to make the 7 indicated multiplications .
There are 5 additions or subtractions of a matrices and the same number of operations on b matrices.
Then, once the results are obtained for the multiplications, they must be reassembled into the product matrix. This requires an additional 8 additions or subtractions of such matrices for each product of same, (according to the rules above for a total of 18 additions or subtractions of 2j by 2j matrices for each multiplication of same.
To handle a 2k by 2k multiplication, we have seen that we must perform
1 2k level product, 7 2k-1 level products, 72 2k-2 level products, and so on.
This will require, as we have noted a total of 7k multiplications of numbers.
And how many additions of numbers?
At level 2k there will be 18 additions each of 22k-2 matrix elements (namely of all the elements of the matrices of half the size of the original matrix (a total of the square of half the size elements) that form the elements of the top level 2 by 2 matrix)
At the next level there will 7/4 as many sums: the 7 comes from there being 7 times as many matrix products that we have to perform, the 4 from the fact that they each have half the size and hence a quarter as many elements.
So the answer is 18*22k-2*(1+ 7/4 + (7/4)2 + …(7/4)k-1) which works out to be
6*(7k-4k).
Thus even the number of additions grows as 6*7k which is 6*nln(7)/ln(2).
This procedure can be implemented on a spreadsheet without too much difficulty for 4 by 4 or 8 by 8 matrices, and with a program you could handle any size.
To do it you must form the 7 combinations of a’s and b’s to be multiplied. Then multiply together the appropriate combinations, then put them in the right places in the resulting matrix. (You have to remember that the coefficient of z12 goes into the 21 element of the product matrix-which is the transpose of what you might think, but that is the only tricky point.)
5. Matrix Magic on a Spreadsheet
The act of matrix multiplication in the ordinary way is easier to implement on a spreadsheet.
In fact it can be accomplished with one instruction suitably copied.
Thus if you enter your k by k matrix A in k rows and columns and put B somewhere next to it, you can place the product AB similarly next to B, by entering the dot product of the first row of A with the first column of B in its upper left corner.
If you put dollar signs on all occurrences of the middle index, (the one summed over) when you copy this entry into the k rows and columns starting from it, you get the product AB, since the other indices will vary and give you the dot product of the rows of A with the columns of B.
But here is where magic occurs. If you copy further to the right, beyond where the matrix AB should be, you find another matrix and another and another.
The spreadsheet iterates the matrix multiplication. So what you get after the product AB is the product of A with it, namely A2B, then A3B, and so on.
And you get all this at the cost only of copying one entry.
You may find this quite mundane, but it seems remarkable to me. But here is something even you will find remarkable.
6.
Determinants and Cofactors with a Spreadsheet
Lewis Carroll, the
author of Alice in Wonderland, was a mathematician and the discoverer of a
useful theorem about determinants.
It can be stated as follows.
Suppose A
is an n by n matrix, and suppose we define Ajk to be the matrix
obtained from A by removing its j-th row and k-th column.
Similarly let us define Ajk,lm to be the matrix obtained from A by omitting
its j-th and k-th rows, and l-th and m-th columns.
We denote the determinant of a matrix by |A|
Carroll’s (or Dodson’s) theorem then takes the form
|A||Ajk ,jk| = |Ajj||Akk| - |Ajk||Akj|.
Here a 0 by 0 determinant is defined to be 1.
The theorem is of particular interest when we choose j=1 and k=n.
It then states that the determinant of a matrix multiplied by the determinant of the matrix obtained by throwing away its outside rows and columns, is the product of the determinants of submatrices obtained by throwing away the top row and left column with the one obtained by throwing away the last row and right column, less the product of the determinant obtained after throwing away the top row and right column and the determinant obtained after throwing away the last row and left column.
This definitely gives the 2 by 2 determinant, and Dodson noticed that it generalizes the 2 by 2 formula to larger matrices.
In fact this theorem can be taken as an inductive definition of te concept of determinant, so long as the determinant of the matrix obtained by throwing away all borders is non-zero.
The most wonderful thing about this theorem is that you can implement it on a spreadsheet with one instruction, and it will, if you start with a matrix of 1’s (representing 0 by 0 determinants) then enter your matrix, then enter one entry and copy it down and across, it will first compute the two by two determinants of submatrices consisting of adjacent rows and columns, then similar 3 by 3 determinants then 4 by 4 etc., until it produces the determinant of your original matrix.
It can fail if you try to divide by a determinant that is 0; but this can be avoided by adding a very small increment appropriately to elements of the original matrix to make all determinants obtained slightly different from 0. By varying these increments if necessary you can eliminate any errors they might introduce.
What is the magic entry?
Choose a blank space q rows below the first column of your matrix, and enter the 2 by 2 determinant of the first two rows and columns of your matrix divided by the entry q-1 rows above the top of your matrix, and one row to its right, (which should be a 1).
You must prepare by filling the squares above your matrix up to the q-1’st row by 1’s.
This algorithm computes the determinant with a cubic number of operations, since it has to compute the sum of 1 + 22 + 32 + . . . (n-1)2 determinants each of which involves two multiplications a subtraction and a division.
In the iteration just before computing the determinant itself, this procedure produces the determinants of matrices obtained by omitting the last row and column, the last row and first column and under these the determinants of matrices obtained by omitting the first row and last column and first row and first column.
These are all plus or minus cofactors of elements in the omitted places.
If you want all the cofactors, you can obtain them by copying columns 1 through n-1 immediately to the right of the n-th column, (you can do that with one instruction (=top left element) copied into the n-1 next columns) and copying the firsr n-1 rows of the resulting matrix (similarly) into the n-1 rows immediately beneath it, before you enter the instruction for your algorithm. You will then have a 2n-1 by 2n-1 square matrix.
This will give you at the end a whole matrix of evaluations of the same determinant, and on the previous iteration will give you the cofactors, up to sign, starting in the second row and second column.
The reason for this is that when you do this at the next to the last iteration each adjacent submatrix will omit exactly one row and column and will be a cofactor of the entry in that row and column, up to a sign. 0.
When n is odd, these values will actually be the cofactors. When n is even, however, the signs of every second one must be reversed to get the cofactors.
Recall that the cofactors of the matrix divided by the determinant give the transpose of the inverse of the matrix. Thus this simple algorithm gives all the information you need to deduce the inverse of the matrix.
Exercises:1. Form a spreadsheet that sets up the matrix multiplication and determinant and inverse finding algorithms described in the last two sections. Use the latter to find the inverse of a random 5by 5 matrix and test it by matrix multiplying it by the original matrix using the former. Arrange to be able to do this for any 5 by 5 matrix which doesn’t cause you to divide by 0.
Another thing you can do is solve n linear equations in n variables by this same method, using Cramer’s Rule. To do this you enter your matrix followed by the right hand side followed by copies of the first n-1 columns of your matrix.
The row in which you compute the n by n determinants of your matrix will contain after it all the numerators you need for Cramer’s rule, though some may have the wrong sign depending on oddness and evenness. From them you can read off the solutions to your linear equations.
To make all this work with large matrices you must take steps to avoid dividing by 0 in your process, (you can get by without it for three by three matrices)
A way to do this that seems to work is to set up a
supplementary matrix of the same shape as what you will handle, and adding it to the
input. This new matrix should be very small (say all entries on the order
of 10-8 in a way that does not produce a 0 determinant easily.
C*ln(j+k) seems to work pretty well for C = 10-8,
where j and k are row and column indices here.